Die Tutorien erläutern die Funktion von IN DUBIO PRO GEO anhand von Praxisbeispielen. Die Lösungen zu den Aufgaben sind mittels vorausgefüllter Formulare nachvollziehbar. In den Auswahlfeldern stehen nicht alle Optionen zur Verfügung. Die Formulare lassen sich mit der Schaltfläche absenden und so die Ergebnisse betrachten. Um das zu ersparen, sind die Ergebnisse im Tutorium auszugsweise dargestellt. Die wesentlichen Zwischen- und Endergebnisse sind durch goldfarbene Boxen hervorgehoben. Die Lösungen sind in weiteren goldfarbenen Boxen kommentiert. Ihre eigene Ausgabe unterscheidet sich möglicherweise in der Darstellung etwas, abhängig von Ihren .

≡ START Anleitung English Aufgabe

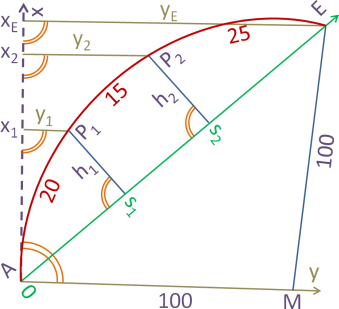
Ein Kreisbogen AP₁P₂E mit dem Radius r=100 soll von A aus abgesteckt werden. Dazu sollen die orthogonalen Absteckmaße der drei Punkte P₁, P₂ und E mit den Bogenlängen AP₁=20, P₁P₂=15 und P₂E=25 bestimmt werden. Diese Absteckmaße sollen sowohl von der Tangente in A aus in Form von x₁, y₁, x₂, y₂, x_E, y_E , als auch zur Kontrolle von der Sehne AE aus in Form von s₁, h₁, s₂, h₂ bestimmt werden.

≡ START Anleitung English Lösung

IN DUBIO PRO GEO Ebene und Kugel : Kreisbögen

Aus zwei oder drei (fast) beliebigen gegebenen Größen eines Kreisbogens werden alle übrigen Größen berechnet, wahlweise einschließlich einer . Bei nur zwei gegebenen Größen wird versucht, so viel wie möglich zu berechnen. Wenn zwei Lösungen existieren, werden beide berechnet.

Winkeleinheit Notiz

Größe	Wert

Probieren Sie es aus: liefert in Auszügen Folgendes:

IN DUBIO PRO GEO Ebene und Kugel : Kreisbögen

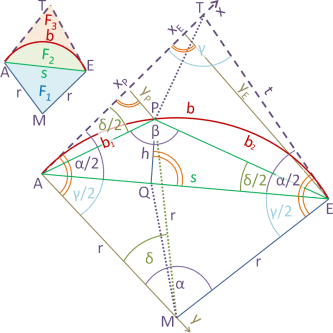
Im ersten Schritt berechnet man P₁ durch eine Kreisbogenberechnung mit b₁=20, b=60 und r=100. P₁ entspricht jetzt P, so dass AQ und h in der linken Tabelle den Werten s₁ und h₁ der Aufgabe entsprechen. Die Tangentenabschnitte x_P, x_E und Tangentenoffsets y_P, y_E entsprechen den gesuchten Absteckmaßen von P₁ und E von der Tangente aus.

Berechnung von P1

Berechnung	Wert
`b₁=START`	20.000000
`b=START`	60.000000
`r=START`	100.00000
`b₂=b-b₁`	40.000000
`α=b/r`	38.197186
`β=π-α/2`	180.90141
`γ=π-α`	161.80281
`δ=b₁/r`	12.732395
`s=2·r·sin(α/2)`	59.104041
`AP=2·r·sin(δ/2)`	19.966683
`PE=2·r·sin((α-δ)/2)`	39.733866
`AQ=AP·cos((α-δ)/2)`	19.568679
`QE=s-AQ`	39.535362
`h=PE·sin(δ/2)`	3.9667676
...	...
`x_P=AP·cos(δ/2)`	19.866933
`x_E=s·cos(α/2)`	56.464247
`y_P=AP·sin(δ/2)`	1.9933422
`y_E=s·sin(α/2)`	17.466439
...	...

IN DUBIO PRO GEO Ebene und Kugel : Kreisbögen

Winkeleinheit Notiz

Größe	Wert

Probieren Sie es aus: liefert in Auszügen Folgendes:

IN DUBIO PRO GEO Ebene und Kugel : Kreisbögen

Im zweiten Schritt berechnet man P₂ durch eine Kreisbogenberechnung mit b₁=35, b=60 und r=100. P₂ entspricht jetzt P, so dass AQ und h in der linken Tabelle den Werten s₂ und h₂ der Aufgabe entsprechen. Die Tangentenabschnitte x_P, x_E und Tangentenoffsets y_P, y_E entsprechen den gesuchten Absteckmaßen von P₂ und E von der Tangente aus.

Größen, die unabhängig vom Punkt P sind, haben identische Werte, wie in der ersten Berechnung.

Man liest also folgende Lösung ab:
x₁=19.87, x₂=34.29, x_E=56.46, s₁=19.57, s₂=34.55
y₁= 1.99, y₂= 6.06, y_E=17.47, h₁= 3.97, h₂= 4.34

Tipp: Sie können Zahlen nicht nur mit Dezimalkomma eingeben, sondern erhalten sie auf Wunsch auch so. (Ausgabedezimaltrennzeichen in auf Komma setzen)

Berechnung von P2

Berechnung	Wert
`b₁=START`	35.000000
`b=START`	60.000000
`r=START`	100.00000
`b₂=b-b₁`	25.000000
`α=b/r`	38.197186
`β=π-α/2`	180.90141
`γ=π-α`	161.80281
`δ=b₁/r`	22.281692
`s=2·r·sin(α/2)`	59.104041
`AP=2·r·sin(δ/2)`	34.821628
`PE=2·r·sin((α-δ)/2)`	24.934947
`AQ=AP·cos((α-δ)/2)`	34.549938
`QE=s-AQ`	24.554104
`h=PE·sin(δ/2)`	4.3413771
...	...
`x_P=AP·cos(δ/2)`	34.289781
`x_E=s·cos(α/2)`	56.464247
`y_P=AP·sin(δ/2)`	6.0627287
`y_E=s·sin(α/2)`	17.466439
...	...

≡ START Anleitung English Rechenprobe

IN DUBIO PRO GEO Ebene und Kugel : Kreisbögen

Winkeleinheit Notiz

Größe	Wert

Probieren Sie es aus: liefert in Auszügen Folgendes:

IN DUBIO PRO GEO Ebene und Kugel : Kreisbögen

Wir berechnen den Kreisbogen AP₁E mit den berechneten Absteckkoordinaten als Eingaben und überprüfen Radius und Bogenlänge. Tatsächlich hat der Kreisbogen den gewünschten Radius und die gewünschte Länge. Auch die Absteckmaße von P₁ von der Sehne aus stimmen. Das bestätigt die Richtigkeit der Rechnung für P₁.

Berechnen Sie genauso den Kreisbogen AP₂E, indem Sie rechts den Wert 19.866933 für x_P durch 34.289781 ersetzen. Ein Vergleich bestätigt die Richtigkeit der Rechnung für P₂.

Rechenprobe von P1

Berechnung	Wert
`x_P=START`	19.866933
`x_E=START`	56.464247
`y_E=START`	17.466439
`s=sqrt(x_E²+y_E²)`	59.104041
`α=2·arcsin(y_E/s)`	38.197188
`β=π-α/2`	180.90141
`γ=π-α`	161.80281
`r=s/2/sin(α/2)`	99.999997
`b=r·α`	60.000000
...	...
`y_P=r±sqrt(r²-x_P²)`	1.9933423
`AP=sqrt(x_P²+y_P²)`	19.966683
`δ=2·arcsin(y_P/AP)`	12.732396
`b₁=r·δ`	20.000000
`b₂=b-b₁`	40.000000
`PE=2·r·sin((α-δ)/2)`	39.733866
`AQ=AP·cos((α-δ)/2)`	19.568679
`QE=s-AQ`	39.535362
`h=PE·sin(δ/2)`	3.9667677
...	...

≡ START Anleitung English Tutorium : Kreisbogenabsteckung

Seiteninhalt

≡ START Anleitung English Aufgabe

≡ START Anleitung English Lösung

IN DUBIO PRO GEO Ebene und Kugel : Kreisbögen

IN DUBIO PRO GEO Ebene und Kugel : Kreisbögen

IN DUBIO PRO GEO Ebene und Kugel : Kreisbögen

IN DUBIO PRO GEO Ebene und Kugel : Kreisbögen

≡ START Anleitung English Rechenprobe

IN DUBIO PRO GEO Ebene und Kugel : Kreisbögen

IN DUBIO PRO GEO Ebene und Kugel : Kreisbögen

≡ START Anleitung English In der Bibliothek