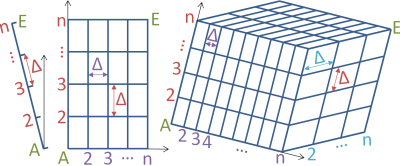
By ''lattice'' we denote the set of regularly arranged points. We avoid the term ''grid'' here because it is used in geodesy for a grid system.
The lattice is defined by a start point A and an end point E. The first created lattice point is the point A and the last one is the point E. If A and E are swapped, you get the same lattice points in opposite succession.
| Lattice | Property | planar or spatial |
|---|---|---|
| line (1D) Read more |
On the connecting line AE, equidistant intermediate points are created. The line may be located arbitrarily oblique in space. | A and E must both be 2D or both be 3D points, and so will be created the intermediate points. |
| rectangle (2D) Read more |
In the axis parallel horizontal rectangle spanned by A and E, equidistant intermediate points are created in both axis directions. | If both A and E are 2D points, so will be created the intermediate points. If A or E has three coordinates, the third coordinates is transferred to all intermediate points. If both A and E are 3D points, the third coordinates must be identical. |
| cuboid (3D) Read more |
In the axis parallel cuboid spanned by A and E, equidistant intermediate points are created in all three axis directions. | A and E must both be 3D points, and so will be created the intermediate points. |
Only for cartesian coordinates (XYZ oder YXZ) the lattice points are always located on spatial straight lines and are equidistant in the sense of Euklid. Otherwise this property is only fulfilled after mapping to the coordinate plane. E.g. for ellipsoidal coordinates (latitude, longitude) they are located on meridians and parallels or on the loxodrome. Exact equidistancy is here obtained only in the equirectangular projection. See type of coordinate system and Loxodrome from Dresden (Saxony) to Dresden (Ontario).
For each line direction (1D lattice) or axis direction (2D or 3D lattice) three input quantities are desired in arbitrary succession. The following five quantities are selectable:
A given edge length must always be combined with exactly one coordinate of A or E. For a negative edge length the lattice points run contrary to the related axis direction, i.e. they start with the largest coordinate.
Point count and lattice spacing should not be zero. Otherwise they are treated as a missing input.
Example: The lattice with the coordinates X=11;21;31;41 can be defined in the following ways:
| XA=11; XE=41; n=4 | XA=11; n=4; l=30 | XA=41; XE=11; n=4 | XA=41; n=4; l=-30 |
| XA=11; XE=41; Δ=10 | XE=41; n=4; l=30 | XA=41; XE=11; Δ=-10 | XE=11; n=4; l=-30 |
| XA=11; n=4; Δ=10 | XA=11; Δ=10; l=30 | XA=41; n=4; Δ=-10 | XA=41; Δ=-10; l=-30 |
| XE=41; n=4; Δ=10 | XE=41; Δ=10; l=30 | XE=11; n=4; Δ=-10 | XE=11; Δ=-10; l=-30 |
| Result: X=11;21;31;41 | Result: X=41;31;21;11 | ||
If the edge length is not an integer multiple of the lattice spacing, the lattice spacing is adapted. So you get the exemplary lattice above also with XA=11; XE=41; Δ=9 or XE=41; Δ=11; l=30.
Also for the grid system, lattice spacing and edge length are in metric scale, i.e. they are not multiplied with the grid scale factor . If this is undesired, please declare the system temporarily as a cartesian system XYZ or YXZ. See also Measurement lists with distances etc. in grid scale .
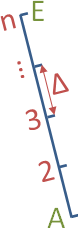
The lattice points are equidistant points on the straight line segment AE, which may be oblique in space. Here the input quantities must always be coordinates of A and B as well as either the point count n or the lattice spacing Δ . The first two columns of the input values must be filled in completely, where the second point count is set to n=1 or the lattice spacing is set to Δ=0 .
The lattice spacing is the spatial separation of the neighboring points. For ellipsoidal systems, the height, if present, is not used for computation of the separation. Siehe Loxodrome from Dresden (Saxony) to Dresden (Ontario).
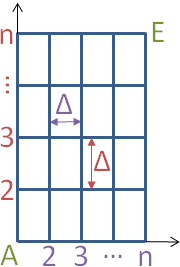
The lattice points are located on the crossings of equidistant coordinate lines, and as such form an axis parallel rectangular lattice. The first two columns of the input values must be filled in completely.
After creation the lattice can be rotated . For different transformations you can transfer the lattice points to . See 2D lattice for the Großer Garten Dresden.
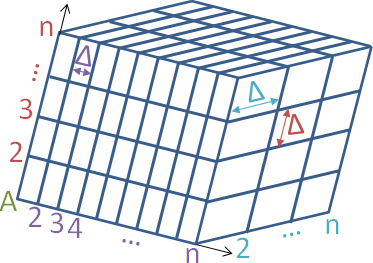
The lattice points are located on the crossings of equidistant coordinate planes, and as such form an axis parallel cuboidal lattice. All nine input values must be given completely. On the canvas only one lattice plane is given (third coordinate fixed).
You can also create a vertical 2D lattice, namely as a 3D lattice with point count n=1 for the first or second coordinate. However, the two corresponding coordinates of A and E must coincide. Moreover, you can also create a vertical 1D lattice by letting the first and second point count be equal to 1 and letting the points A and E differ only in the third coordinate. However, the same lattice is obtained more directly as a true 1D lattice.
After creation the lattice can be rotated about a vertical axis. For different transformations you can transfer the lattice points to .
The first created lattice point is the point A and the last one is the point E. If A and E are swapped, you get the same lattice points in opposite succession.
The created lattice points are collected to a coordinate list . You define a system name and a type of system . The column format is always ''coordinates'', such that the created lattice points are automatically named . Lattice point lists can be saved and processed by other computation tools, e.g. they may be rotated.
This rotation is not possible for ellipsoidal coordinates (latitude, longitude). Otherwise, you can choose, if lattice points should be rotated about a vertical axis (parallel to z axis), and about which point. The following are selectable:
After creation of the axis parallel lattice or 1D lattice you specify the angle of rotation between -π = -180° = -200 gon and π = 180° = 200 gon. Before you should have selected the angle unit in the . Rotations are defined
The viewing direction for this is opposite to the rotation axis, i.e. from above.
For different transformations, e.g. rotations about other axes or shear mappings, you can transfer the lattice points to and configure arbitrary transformation steps and parameters.
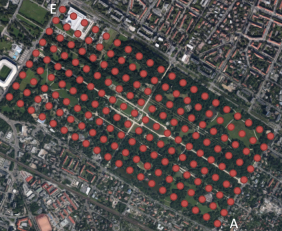
The Großer Garten Dresden has a nearly rectangular shape with edge lengths 1900 m and 950 m. The northernmost vertex has the UTM coordinates (zone 33U) easting = 412734 m and northing = 5655664 m. The azimuth of the short edge is 35 gon ≈ 31°. A lattice with the lattice spacing 190 m must be computed.
Firstly, for the type of grid system Easting Northing Height you create an axis parallel 2D lattice on a rectangle with edge lengths 1900 m; 950 m and the lattice spacings 190 m in both axis directions. For the lattice to end at the northermost point E, you may give the first edge length and the first lattice spacing negative, such that the first coordinate (east) runs opposite to the axis direction. After creation you obtain 11×6=66 lattice points. Finally, you must rotate the lattice by 31° about edge point E.
We consider the following points in ellipsoidal coordinates referring to :
| ellipsoidal | |||
|---|---|---|---|
| point | latitude | longitude | height |
Dresden
(Saxony), centre point of the central building of the 
| 51.037512° | 13.735186° | 120 m |
| Dresden (Ontario), St. Andrews Presbyterian Church | 42.590278° | -82.181667° | 183 m |
The loxodrome connecting these points should be realised by intermediate points. For the distance of the intermediate points we choose 1°.
See for yourself that the created points are not equidistant on the ellipsoid, by transferring the 97 points to and computing as a polyline. The side lengths vary between 70826 m and 82532 m. Moreover, you see that the loxodrome is not the shortest path between the points on the ellipsoid, because all polygonal angles are smaller than π = 180° = 200 gon. The smallest polygonal angle is the first, which amounts to only 199.12 gon = 179.21°.
Instead of this we have created equidistant intermediate points on a straight line in equirectangular projection. To prove this, transfer the created points to a coordinate list and change the system type to XYZ or YXZ before saving. Now transfer the saved list to and compute as a polyline. The heights are now ignored. The side lengths are now all equal to 1.0030010552°. The difference to the desired value Δ=1° is due to the fact that the specified point spacing was not an integer multiple of the point distance, such that the spacing had to be slightly adapted. All planar polygonal angles are now exactly equal to π = 180° = 200 gon.
Now, also load the list to to see that the points are equidistant also in 3D space. The distance of 1.1986138574 is now, however, a strange mixture of degree and metre. All polygonal angles are again exactly equal to π = 180° = 200 gon.
Compare the solutions of these exercises with Points on the geodesic from Dresden (Saxony) to Dresden (Ontario).
|
|
|
|