Seiteninhalt

Genauigkeitsmaße Anwendung von Fortpflanzungsgesetzen Kreisbogenradius Fehlerfortpflanzung mit dem Universalrechner und mit Trilateration Bogenschnitt In der Bibliothek

≡ START Erste Schritte English

In der Geodäsie werden nicht nur unbekannte Größen berechnet, sondern es wird auch abgeschätzt, wie genau oder ungenau diese Größen erhalten werden. Berechnete Größen erben ihre Abweichungen, die sogenannten Fehler, von den Größen, aus denen sie berechnet werden. Diese Größen können gemessen sein und Messabweichungen besitzen oder aus anderen Größen berechnet sein und so ihre Abweichungen wiederum geerbt haben. Man sagt, die Fehler pflanzen sich fort. Sowohl Verstärkung, als auch Abschwächung von Fehlern sind möglich.

Es ist wichtig, diese Fehlerfortplanzung rechnerisch zu vollziehen, um

1. die Genauigkeiten berechneter Größen anzugeben,
2. die den Vorgaben entsprechende erforderliche Genauigkeit von Messwerten zu bestimmen und
3. Messungsanordnungen zu optimieren.

Diese drei Ziele werden durch Anwendung von Fortpflanzungsgesetzen erreicht.

≡ START Erste Schritte English Genauigkeitsmaße

Genauigkeiten können auf verschiedene Art durch Maßzahlen ausgedrückt werden. IN DUBIO PRO GEO arbeitet mit den folgenden drei Genauigkeitsmaße:

Standardabweichung	Std	früher auch mittlerer Fehler genannt
maximale absolute Abweichung	Max	größtmöglicher Fehler
Gewicht	Gew	ein relatives Genauigkeitsmaß

In der Geodäsie ist die Standardabweichung verbreitet, weil die maximale absolute Abweichung schwer abschätzbar ist oder oft Werte ergibt, die zwar theoretisch möglich sind, aber nur durch Verkettung extrem ungünstiger Umstände.

• Genauigkeitsmaße dürfen nicht negativ sein, und Gewichte dürfen auch nicht Null sein.
• Bei fehlenden Maßen gelten die zugehörigen Größen als fehlerfrei.
• Abweichungsmaße dürfen nicht beliebig groß sein, andernfalls werden sinnlose und im Extremfall auch gar keine Ergebnisse erhalten, sondern eine Fehlermeldung.

Ein einfacher Test, ob Abweichungen ausreichend klein sind, besteht darin, die Berechnung mit den halben Genauigkeitsmaßen zu wiederholen und zu überprüfen, ob sich auch alle berechneten Maße etwa halbieren.

≡ START Erste Schritte English Anwendung von Fortpflanzungsgesetzen

Für jedes Genauigkeitsmaß gibt es ein eigenes Fortpflanzungsgesetz. Finden Sie die theoretischen Grundlagen hier erläutert:

Hat man zu jeder ungenauen Startgröße eine zugehöriges Genauigkeitsmaß, dann können bei einigen Rechenwerkzeugen ( ) diese Maße angegeben und die entsprechenden Genauigkeitsmaße aller berechneten Größen erhalten werden. IN DUBIO PRO GEO wendet hierzu ein Fortpflanzungsgesetz an. Voraussetzung dafür ist, dass die Startgrößen statistisch unkorreliert sind. Das bedeutet praktisch, dass diese Genauigkeitsmaße letztlich aus zufälligen Messabweichungen resultieren, wobei jede dieser Messabweichungen aber nur höchstens eine Startgröße beeinflusst.

≡ START Erste Schritte English Kreisbogenradius

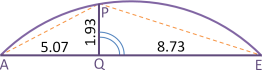
Wie genau lässt sich durch Messband-Messung der Sehnenabschnitte AQ und QE und der Pfeilhöhe PQ der Radius des Kreisbogens in der Abbildung bestimmen? Aus Erfahrung erhalten wir für alle drei Messwerte eine Standardabweichung von je 0.03 . Das Ergebnis ist ein Radius von 12.57 mit einer Standardabweichung von 0.18.

und Rechnen

Wenn wir statt dessen oder zusätzlich eine maximale absolute Abweichung der Messbandmessungen von je 0.1 annehmen, so erhalten wir eine maximale absolute Abweichung für den Radius von 0.86.

und Rechnen

In beiden Fällen werden die Abweichungen deutlich verstärkt. Dieser Effekt ist bei noch flacheren Bögen, wie sie praktisch z.B. im Verkehrswegebau vorkommen, noch stärker.

Wenn wir hingegen nicht sicher wüssten, welche Standardabweichungen den Messband-Messungen zugeordnet werden können, sondern nur, in welchem Verhältnis diese zueinander stehen, können wir mit Gewichten arbeiten. Sind diese Standardabweichungen alle gleich, wählen wir für alle Messwerte das Gewicht 1 und berechnen eine Gewichtsfortpflanzung. Als Ergebnis erhalten wir für den Radius das vergleichsweise geringe Gewicht 0.028, welches zumindest auf eine ungünstige Fehlerfortpflanzung hinweist.

und Rechnen

Würden wir versuchen, den Radius durch Messung der langen Sehne AE und der beiden kurzen Sehnen AP und PE (⇑ Abbildung) mit derselben Genauigkeit, also demselben Gewicht 1 zu bestimmen, erhielten wir durch Gewichtsfortpflanzung für den Radius das noch viel geringere Gewicht 0.0034. Diese Messungsanordnung ist also noch weniger empfehlenswert.

und Rechnen

Interessant auch, dass man alle diese Rechnungen genauso gut mit machen kann. Berechnet wird das Dreieck AEP. Der Kreisbogenradius entspricht dem Umkreisradius dieses Dreiecks. Als Beispiel hier die erste Berechnung mit dieser Version:

und Rechnen

≡ START Erste Schritte English Fehlerfortpflanzung mit dem Universalrechner und mit Trilateration

Obwohl der keine direkte Funktion zur Fehlerfortpflanzung anbietet, ist es möglich, auch hier auf geschickte Weise eine Fehlerfortpflanzung zu berechnen: Nehmen wir an, wir haben n ungenaue Startgrößen (Koordinaten und/oder Messwerte). Man lässt die Rechnung n+1-mal ausführen, einmal mit unveränderten Startwerten und n-mal mit je einem um seine Standardabweichung oder maximale absolute Abweichung veränderten Startwert, einem nach dem anderen. Dann zieht man die Differenzen Δ_i der interessierenden Ergebnisse in Bezug zur ersten Rechnung nach dem Fehlerfortpflanzungsgesetz zusammen:

für Standardabweichungen:	σ²= Δ1² +…+ Δn²
für maximale absolute Abweichungen:	Δ=|Δ1|+…+|Δn|

Wenn man die Punkte mit veränderten Koordinaten anders benennt und an die Koordinatenliste anhängt und wenn man auch den n+1 Ergebnissen für die Neupunkte jeweils andere Punktnamen zuweist, kann man die n+1 Rechnungen im in einem einzigen Rechengang ausführen lassen.

Dasselbe funktioniert genauso auch mit dem Rechenwerkzeug .

≡ START Erste Schritte English Bogenschnitt

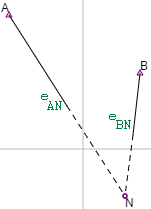
Betrachten wir z.B. einen Bogenschnitt mit zwei Festpunkten A und B und einem Neupunkt N sowie zwei gemessenen Horizontaldistanzen e_AN = 11.436; e_BN = 6.576. Alle vier Lagekoordinaten haben Standardabweichungen von 0.03 und beide Distanzen haben Standardabweichungen von 0.01. Damit haben wir 6 ungenaue Startgrößen X_A,Y_A, X_B,Y_B,e_AN,e_BN. Die Liste der bekannten Punkte kann also lauten:

      Y     X
A   16.10 17.11 // unveränderter Punkt
B   23.06 14.02 // unveränderter Punkt
AY  16.13 17.11 // Y-veränderter Punkt A
BY  23.09 14.02 // Y-veränderter Punkt B
AX  16.10 17.14 // X-veränderter Punkt A
BX  23.06 14.05 // X-veränderter Punkt B

Nun berechnen wir die 7 Bogenschnitte in einem einzigen Rechengang mit dem und gibt den 7 Ergebnissen für den Neupunkt jeweils die Punktnamen N,N1,N2,…,N6 . Jeder Bogenschnitt hat zwei Lösungen. Diese kombinieren sich zu insgesamt 2⁷=128 Lösungen. Es reicht aber, nur die erste zu betrachten. Alle anderen Lösungen ergeben dieselben Genauigkeiten.

und Rechnen mit

und Rechnen mit

Man kann sich leicht ein Bild von der räumlichen Verteilung der 7 berechneten Punkte machen, wenn man diese in einer Koordinatenliste speichert und auf der Leinwand betrachtet. Die größten Einflüsse stammen von den X-Koordinaten der Anschlusspunkte A (→N1), B (→N3):

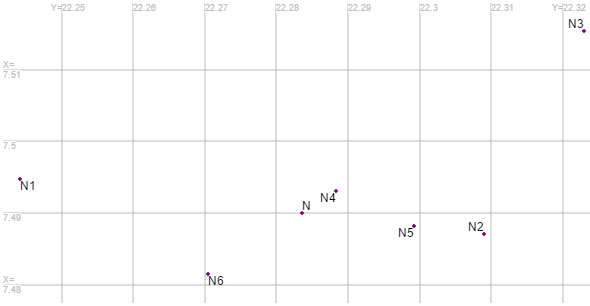
Nun müssen die Differenzen Δ_i berechnet werden. Unterstützen kann man dies durch Laden der Punkte in und Berechnung einer Translation, so dass N in den Nullpunkt des Koordinatensystems verschoben wird. Die transformierten Koordinaten der anderen 6 Punkte sind unmittelbar die gesuchten Differenzen. Schließlich erhalten wir für den Neupunkt N durch Anwendung des Fehlerfortpflanzungsgesetzes für Standardabweichungen:

σ_Y=(0.039²+0.025²+0.039²+0.005²+0.016²+0.013²)^½=0.065
σ_X=(0.005²+0.003²+0.025²+0.003²+0.002²+0.008²)^½=0.028

Wären die gegebenen Abweichungen absolute Abweichungen gewesen, würde sich statt dessen durch Anwendung des entsprechenden Fehlerfortpflanzungsgesetzes ergeben:

Δ_Y=0.138; Δ_X=0.047

In beiden Fällen verstärken sich die Abweichungen vor allem in der Y-Koordinate von N.

Schon gewusst? Platzieren Sie den Mauszeiger über die mit markierten Begriffe, um deren Bedeutung zu erfahren.

≡ START Erste Schritte English