
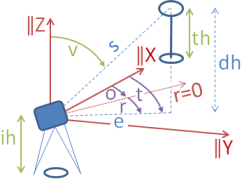
Punktkoordinaten können kartesische oder Gitterkoordinaten sein und werden hier unterschiedslos mit X,Y,Z bezeichnet. Polare Messwerte können sein:
Die Kombination der gegebenen Koordinaten und Messwerte kann völlig beliebig sein. Es wird immer berechnet, was sich mit den vorhandenen Größen berechnen lässt, und zwar vollständig . Auch können alle Messwerte fehlen und nur Stand- und Zielpunktnamen angegeben sein. Es wird dann versucht, Polarwerte aus gegebenen Koordinaten zu berechnen. Polarwerte aus kartesischen Koordinaten berechnen
Wenn verschiedene Rechenwege zu denselben Größen führen, werden alle durchgerechnet und verglichen. Es werden Anzahl, Minimum und Maximum sowie die Quartilabstand (IQR) sowie Spannweite der je Größe erhaltenen Werte berechnet. Sind IQR oder Spannweite gering, sollte der Median als endgültiges Ergebnis in Betracht gezogen werden, andernfalls ist ein grober Fehler in den Startwerten wahrscheinlich. Ausreißererkennung. Bei vielen verschiedenen Werten wird der Median kaum von einzelnen groben Fehlern in den Eingabewerten verfälscht. Es erfolgt keine Ausgleichung im herkömmlichen Sinne nach kleinsten Quadraten, aber die Ergebnisse sind sehr gut kontrollierbar und sogar ausgeglichen im Sinne einer robusten Schätzung.
Manchmal werden mathematisch äquivalente Rechenwege gefunden. Die zugehörigen Ergebnisse sind gleich, werden aber als separate Werte aufgeführt. Das beeinflusst möglicherweise die Berechnung des Medians.
Wenn ausreichend viele verschiedene Rechenwege für eine Größe gefunden wurden, wird untersucht, ob sich IQR oder Spannweite der erhaltenen Werte verringern lassen, indem ungünstige geodätische Schnitte (sogenannte ''schleifende'' Schnitte) oder ungünstige Berechnungen in sehr spitzwinkligen Dreiecken vermieden werden. Ist das der Fall, werden die entsprechenden Werte verworfen. Die Gesamtzahl der verworfenen Werte wird dokumentiert. Im Beispiel Unzugänglicher Punkt mit horizontalen Hilfsdreiecken wurden 1292 von 2590 berechneten Werten wegen ungünstiger Schnittwinkel verworfen.
Der Systemtyp der Koordinaten der bekannten Punkte muss kartesisches Linkssystem oder Gittersystem sein. An die Distanzen müssen die Instrumentenkorrektionen wie Additions- bzw. Prismenkonstanten angebracht sein, aber nicht der Gittermaßstabsfaktor.
Bei bekannten Punkten müssen immer mindestens beide Lagekoordinaten X,Y oder Nordwert, Ostwert vorhanden sein.
Fehlende Koordinaten und Messwerte gelten immer als unbekannt, also auch fehlende Instrumentenhöhen ih und Zielhöhen th ! Werden z.B. Höhen für Neupunkte benötigt, so müssen Instrumenten- und Zielhöhen vollständig angegeben werden.
Wann immer das möglich ist, werden Startwerte standardmäßig auch aus anderen Startwerten neu berechnet. Das ermöglicht auch hier eine Kontrolle auf grobe Fehler. Möchte man hingegen einzelne Startwerte als fehlerfrei definieren, so kann man die Neuberechnung der Startwerte auch unterdrücken. Das kann man für alle Punktkoordinaten (nur XY oder nur Z oder XYZ), für alle polaren Messgrößen (rtesvo…) oder für alle Startgrößen (XYZrte…) tun. Diese Optionen helfen auch, bei umfangreichen Rechnungen den Überblick zu behalten.
Mit diesem können auch ausgewertet werden. Allerdings werden keine Instrumentenfehler und keine Genauigkeitsmaße berechnet. Deshalb empfehlen wir, das Rechenwerkzeug zu benutzen. Sie können die dort erhaltenen Satzmittel direkt in diesen laden.
Oft berechnet der nur polare Werte zwischen Punkten, zwischen denen gemessen wurde (Stand- und Zielpunkte in einer Aufstellung). Mehr Ergebnisse erhält man manchmal, wenn man bei einzelnen Standpunkten noch blinde Zielpunkte ohne Messwerte hinzufügt. Möchte man z.B. die Horizontaldistanz zwischen zwei bekannten oder berechneten Punkten erhalten, gibt man diese irgendwo als Stand- und Zielpunkte ohne Messwerte an. Von diesem Wert würde auch in weiteren Rechnungen Gebrauch gemacht, wenn er irgendwo nützlich ist. Finden Sie einen solchen Fall im Beispiel Polarwerte aus kartesischen Koordinaten berechnen.
Die Gesamtzahl von Startwerten (gegebene Punktkoordinaten und polare Messwerte) ist auf 256 begrenzt. Diese sind wie folgt zu zählen:
Die Startwerte werden in zwei Gruppen unterteilt:
Die Anzahl der tatsächlich verwendeten Startwerte wird dokumentiert.
Die Gesamtrechenzeit ist auf 90 s und der Gesamtspeicherbedarf ist auf 128 MB begrenzt. Weil eine aufwendige Suche nach allen möglichen Rechenwegen erfolgt, dauert eine vollständige Lösung bei vielen Startwerten manchmal lange. Die Rechenzeit kann auch durch den Nutzer stärker begrenzt werden. Wird bei großen Rechnungen diese Grenze letztlich erreicht, dann werden nicht alle theoretisch möglichen Werte berechnet, aber immer noch so viele, dass ein zuverlässiges Ergebnis im Sinne einer robusten Schätzung erhalten wird. Eine Warnung wird erzeugt. Es ist damit aber nicht gesagt, dass eine längere Rechenzeit tatsächlich auch mehr Ergebnisse produzieren würde.
Wird eine dieser Grenzen überschritten, versuchen Sie, die Aufgabe zu splitten. Die Rechenzeit verringert sich auch erheblich, wenn Sie die Neuberechnung der Startwerte unterdrücken.
Nachfolgend skizzieren wir den Universalrechner-Algorithmus. Wenn Sie diese Information nicht benötigen, überspringen Sie diesen Abschnitt einfach.
Wenn eine Berechnung mehrere Lösungen ergab, ist das Aufrufen der momentan nicht dargestellten Lösungen nur sofort nach dem Rechnen möglich. Wenn zwischendurch der Rechenablauf analysiert oder eine Ausreißererkennung gestartet wurde oder die Ergebnistabelle sortiert wurde, verschwinden die Schaltflächen für das Anzeigen dieser Lösungen. Abhilfe schafft eine nochmalige Berechnung.
Alle berechneten Größen werden in einer Tabelle dargestellt, sortiert nach Größenarten. Innerhalb der Größenarten wird nach (Stand-)Punktnamen sortiert, oder wahlweise nach Medianen, IQRs oder Spannweiten (kleinste zuerst). Spannweiten werden nur angezeigt, wenn nach ihnen sortiert wird, und ersetzen dann in der Tabelle die IQR-Werte. Bei Lagekoordinaten wird je Punkt immer X und Y zusammenhängend aufgelistet. Bei der Sortierung nach IQRs ist bei X und Y die Summe beider IQRs entscheidend. Dasselbe gilt für Spannweiten, wenn danach sortiert wurde.
Richtungswinkel t und Horizontaldistanzen e werden immer nur in einer Richtung angegeben, und zwar so, dass die beiden Punktnamen lexikographisch sortiert sind. Für die Gegenrichtung ändern Sie t um π = 180° = 200 gon. Höhendifferenzen dh und Schrägdistanzen s in Sicht und Gegensicht könnten differieren, wenn die zugehörigen Instrumenten- und Zielhöhen nicht gleich sind.
Die Spalte Werte zeigt an, wieviele Werte für jede berechnete Größe erhalten wurden. Bei Lagekoordinaten eines Punktes sind die Werte immer gleich und werden nur einmal angegeben. Ggf. verworfene ungünstige Schnitte und ∄-Ergebnisse (keine Zahl) zählen nicht mit. Eine Startgröße, die zusätzlich x mal berechnet wurde, erscheint als 1+x.
Den Rechenablauf können Sie detailliert nachvollziehen. Wenn Sie das nicht wollen, überspringen Sie diesen Abschnitt. Klicken Sie für eine interessierende Größe auf die Zahl(en) in Spalte Werte um die detaillierte Dokumentation des Rechenablaufs und der Einzelwerte angezeigt zu bekommen.
Zusätzlich zu den in der genannten Symbolen für die Messwerte werden hier folgende Abkürzungen verwendet. Die Tabelle zeigt auch, welche Ergebnisse die Rechenschritte produzieren können.
| Symbol | Rechenschritt | eindeutig | zweideutig | ung. Schnitt | keine Zahl |
|---|---|---|---|---|---|
| Rec2Pol/ Pol2Rec | Koordinatenumwandlung kartesisch⇔polar | X | |||
| BS | Bogenschnitt | X | X | X | |
| GK | Gerade-Kreis-Schnitt | X | X | X | X |
| VS | Vorwärtsschnitt | X | X | X | |
| RS | Rückwärtsschnitt | X | X | X |
Angenommen, die Winkeleinheit ist gon . Ein Rechenschritt wird z.B. dokumentiert wie:
t(P1→3)7 = r(3°2→P1) + o(3°2)3 ± 200 = 69.965792398379
Das kann wie folgt gelesen werden: Der 7. Wert des Richtungswinkels t von Punkt P1 nach Punkt 3 wird aus der gegebenen Horizontalrichtung r (Index fehlt → Startwert) gemessen in der zweiten Aufstellung auf Standpunkt 3 nach Punkt P1 und dem 3. berechneten Wert des Orientierungswinkels o für die zweite Aufstellung auf Standpunkt 3 berechnet. Das Ergebnis lautet 69.965792398379 in der gewählten Winkeleinheit Gon . Gibt es pro Standpunkt nur eine Aufstellung, entfällt der Aufstellungszähler nach dem Standpunktnamen. Oder z.B.:
XY(2)9 = VS(XY(1)5,t(1→2)2,XY(Q3),t(2→Q3)4) = ∄
Das kann wie folgt gelesen werden: Die 9. berechneten Werte der Lagekoordinaten XY von Punkt 2 werden mittels Vorwärtsschnitt (VS) aus den 5. Werten der berechneten Koordinaten XY von Punkt 1 , aus dem 2. berechneten Wert des Richtungswinkels t von Punkt 1 nach Punkt 2 , aus den gegebenen Werten der Koordinaten XY (Index fehlt → Startwerte) von Punkt Q3 und aus dem 4. berechneten Wert des Richtungswinkels t von Punkt 2 nach Punkt Q3 berechnet. Das Ergebnis lautet ∄ (keine Zahl), weil aufgrund von groben Fehlern in den Startwerten kein reeller Schnitt der Strahlen entsteht.
In der Dokumentation des Rechenablaufs werden auch die wegen ungünstiger Schnitte verworfenen Werte dargestellt.
Wenn genügend viele Werte pro berechenbare Größe erhalten wurden, d.h. wenn die Redundanz hoch genug ist, kann versucht werden, Ausreißer in den Startwerten (Koordinaten und Messwerte) zu erkennen. Unter der Ergebnistabelle erscheint dann die Schaltfläche . Wenn Sie diese klicken, werden die Ergebnisse auf Ausreißer untersucht.
Diese Ausreißererkennung zeigt, was passieren würde, wenn ein Startwert eliminiert und die Berechnung wiederholt würde. Dadurch würden weniger Ergebnisse erhalten, die verbleibenden wären aber unverändert. Dadurch verringerten sich oft für einige Ergebnisgrößen die IQRs und Spannweiten. Einen Ausreißer erkennt man an einer drastischen Verringerung dieser Werte. Beachten Sie, dass zur Ausreißererkennung die Spannweiten vor der Vermeidung ungünstiger Schnitte herangezogen werden.
Die Ausreißererkennung erzeugt eine nach den einzelnen Spalten sortierbare Tabelle mit folgenden Informationen je Startwert:
| noch berechen- bare Größen |
Es ist möglich, dass nach Eliminierung eines Startwertes einige Größen nicht mehr berechenbar sind. Die Tabelle zeigt, wieviel Prozent der Größen noch berechenbar sind. Startgrößen, für die kein zweiter Wert mehr berechnet werden kann, zählen hier als nicht mehr berechenbar. 100% bedeutet: Nach der Eliminierung können immer noch alle Größen wenigstens einmal berechnet werden. |
|---|---|
| noch berech- enbare Werte |
Nach der Eliminierung eines Startwertes sind nicht mehr alle Werte berechenbar. Die Tabelle zeigt, wieviel Prozent der Werte noch berechenbar sind. Ist diese Zahl klein, so ist der Startwert für eine zuverlässige Lösung sehr wichtig und eine Eliminierung ist fragwürdig. |
| kleinere Spannweiten |
Die Tabelle zeigt, wieviel Prozent der Spannweiten sich nach Eliminierung eines Startwertes verringern. Ist diese Zahl groß, so ist der Startwert wahrscheinlich ein Ausreißer. |
| maximale Reduktion |
Die Tabelle zeigt, um wieviel Prozent sich eine Spannweite maximal reduziert. Ist diese Zahl groß, so ist der Startwert wahrscheinlich ein Ausreißer. |
| Ausreißerwahr- scheinlichkeit |
Die Wahrscheinlichkeit, dass ein Startwert ein Ausreißer ist, wird abgeschätzt. Selbst wenn mehrere Startwerte als wahrscheinliche Ausreißer ausgewiesen werden, bedeutet das nicht, dass alle Ausreißer sind. Es könnte auch nur einer von ihnen sein. |
Falls in der Tabelle Startgrößen fehlen, können diese wegen zu geringer Redundanz nicht auf Ausreißer untersucht werden. Ist die Gesamtredundanz gering, scheitert die Ausreißersuche manchmal. Eine Fehlermeldung wird erzeugt.
Nun kann ein zu eliminierender Startwert selektiert werden (1. Spalte der Ausreißertabelle). Ein Kandidat ist schon vorselektiert. Ein Klick auf die Schaltfläche stellt die Ergebnisse neu dar, die verbleiben, nachdem der selektierte Startwert eliminiert wurde. (Die eigentliche Berechnung wird nicht wiederholt.) Der eliminierte Startwert erscheint zwar weiterhin in der Liste der bekannten Punkt oder der Eingabe-Messwerte, wird aber nun nicht mehr benutzt. Falls die Redundanz immer noch ausreicht, kann erneut eine Ausreißererkennung verlangt werden, usw.
Eine Anwendung der Ausreißererkennung finden Sie im Beispiel Trigonometrischer Höhenzug.
Die Punkte eines Fußballfeldstrafraums 1,2,3,4,5,6 sollen mit einem Tachymeter, welches über den Eckpunkten A,B des Feldes aufgebaut wird, abgesteckt werden. Die Instrumentenhöhen sind 1.42 m über A und 1.55 m über B. Über den Zielpunkten wird ein Absteckreflektor der Höhe 0.15 m aufgehalten. Gesucht sind die abzusteckenden Polarwerte: Richtungswinkel t, Schrägdistanzen s und Zenitwinkel v der sechs abzusteckenden Punkte.
Zunächst definieren wir ein Koordinatensystem, am besten ein kartesisches Linkssystem YXZ und bestimmen die kartesischen Koordinaten aller Punkte A,B,1,...,6 in diesem System in Meter. Wie man aus der Abbildung abliest, hat der Punkt 6 beispielsweise die X-Koordinate 75.00/2-7.32/2-5.50-11.00=17.34 und die Y-Koordinate 5.50+11.00=16.50. Als Höhen verwenden wir generell 0.00. Nun legen wir die an.
Die besteht aus zwei Standpunkten A und B. Die Standpunktzeilen müssen die Instrumentenhöhen 1.42 und 1.55 enthalten. Weil alle Zielpunkte dieselben Zielhöhen 0.15 haben, können wir diese als Ausfallzielhöhe (Ausfallwert für die Zielhöhe) in der Standpunktzeile notieren und in den Zielpunktzeilen weglassen. Die Zielpunktzeilen enthalten dann nur noch die Namen der Zielpunkte. Das für die leeren Spalten gewählte Format ist bedeutungslos, kann z.B. ''Code/nicht benutzt'' sein.
Die Verarbeitungsmaschine sucht nach berechenbaren Größen und findet Höhendifferenzen dh , Horizontaldistanzen e, Schrägdistanzen s , Richtungswinkel t und Zenitwinkel v , allerdings nur für die gemessenen Visuren. Zwischen den Zielpunkten untereinander wird nichts berechnet. Wird z.B. die Distanz zwischen 1 und 3 gewünscht, müsste ein weiterer Standpunkt 1 mit Zielpunkt 3 ( blinder Zielpunkt ) notiert werden, oder umgekehrt.
Außerdem erhalten wir die Richtungswinkel hier nur vom Zielpunkt zum Standpunkt. Das liegt daran, dass Richtungswinkel und Horizontaldistanzen immer so angegeben werden, dass die beiden Punktnamen lexikographisch geordnet sind. Ziffern kommen hierbei vor Buchstaben. Man muss also den Richtungswinkel um 200 gon ändern. Um trotzdem die Richtungswinkel in Zielrichtung ausgegeben zu bekommen, könnte man die Punkte umbenennen, z.B. von 1 in P1 usw. Eine andere Möglichkeit besteht darin, die Ausgabe von Richtungen zu erzwingen. Diese werden immer vom Standpunkt zum Zielpunkt erhalten. Hierzu muss jeder Standpunkt nur noch um den Orientierungswinkel 0 erweitert werden.
Schließlich erhalten wir nach sinnvoller Rundung folgende polaren Absteckwerte in Meter und Gon:
| s | t | v | s | t | v | |||
|---|---|---|---|---|---|---|---|---|
| A→1 | 47.000 | 7.470 | 101.720 | B→1 | 28.903 | 187.797 | 103.085 | |
| A→2 | 28.897 | 12.203 | 102.799 | B→2 | 47.004 | 192.530 | 101.896 | |
| A→3 | 39.101 | 18.165 | 102.068 | B→3 | 39.105 | 181.835 | 102.280 | |
| A→4 | 59.988 | 17.743 | 101.348 | B→4 | 23.977 | 151.580 | 103.719 | |
| A→5 | 42.590 | 31.390 | 101.899 | B→5 | 42.594 | 168.610 | 102.093 | |
| A→6 | 23.970 | 48.420 | 103.375 | B→6 | 59.991 | 182.257 | 101.486 |
Falls gewünscht, können auch andere Absteckwerte der Ergebnistabelle entnommen werden, z.B. e oder dh.
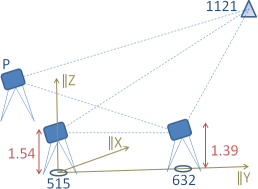
Ein unzugänglicher Punkt 1121 wurde von drei Tachymeterstandpunkten 515,632,P gemessen. Die Höhe des Punktes 515 beträgt 107.483 m, die Instrumentenhöhe ist hier 1.54 m. Die Höhe des Punktes 632 beträgt 107.832 m, die Instrumentenhöhe ist hier 1.39 m. Die Höhe des Hilfspunktes P ist unbekannt, die Instrumentenhöhe kann hier auf einen beliebigen Wert gesetzt werden, sagen wir 0.00 m. Die Zielhöhen sind jeweils gleich den Instrumentenhöhen auf demselben Punkt, weil zueinander passende Instrumente und Reflektoren verwendet wurden. Der Punkt 1121 wurde direkt angezielt ohne Distanzmessung, so dass die zugehörige Zielhöhe 0.00 m beträgt. Die Höhe des Punktes 1121 kann in beiden Hilfsdreiecken 515,632,1121 und P,632,1121 berechnet werden. Die Messwerte sind:
| Stand- | Ziel- | Horiz.- | Zenit- | Schräg- |
|---|---|---|---|---|
| punkt- | punkt- | richtung | winkel | distanz |
| name | name | [gon] | [gon] | [m] |
| 515 | 1121 | 149.846 | 91.886 | --- |
| 632 | 187.807 | 99.991 | 952.233 | |
| 632 | 515 | 260.607 | 100.018 | 952.233 |
| P | 260.740 | 100.086 | 941.461 | |
| 1121 | 314.405 | 89.258 | --- | |
| P | 1121 | 28.449 | 91.684 | --- |
| 632 | 66.940 | 99.923 | 941.461 |
Da reine Höhenfestpunkte nicht unterstützt werden, muss ein lokales Koordinatensystem angelegt werden, am besten ein kartesisches Linkssystem XYZ. Zunächst benötigen wir die Horizontaldistanz 515→632. Dazu kann eine einfache Rechnung wie im vorigen Beispiel mit dem angestellt werden. Das Ergebnis ist 952.233, genau wie die Schrägdistanz von 515→632, weil beide Punkte fast dieselbe Höhe haben. Wir definieren X515=1000, Y515=1000, X632=1000, Y632=1952.233. Damit verläuft die definierte Y-Achse parallel zur Projektion von 515→632 in die Horizontalebene. Nun legen wir die und die an. Für die nicht gemessenen Distanzen zum unzugänglichen Punkt 1121 wurde 0 notiert. Denselben Effekt hätte ein negativer oder nicht-numerischer Wert. Eine alternative Notation eines nicht gemessenen Wertes kann mit der '';;''-Methode erfolgen, siehe Tabellarische Datensätze.
Im Ergebnis werden 49 Größen mit insgesamt 2590 verschiedenen Werten erhalten. Davon werden 1292 Werte wegen ungünstiger Schnittwinkel verworfen. Für die Höhe Z des unzugänglichen Punktes 1121 werden nicht weniger als 52 verschiedene Lösungen berechnet. Der IQR-Wert wird mit 7 mm erhalten, was plausibel ist, der Median beträgt 2201,111 m.
Folgendes sollten Sie beachten:
Dasselbe Beispiel wird auch für Höhennetze
benutzt und kann damit bearbeitet werden.
Die Ergebnisse sind allerdings nicht völlig identisch, weil
eine Ausgleichung nach kleinsten Quadraten durchführt, wobei auch die Standardabweichung von 1.4 mm erhalten wird.
Die Abweichung in der endgültigen Höhe des unzugänglichen Punktes 1121 beträgt nur 0.43 mm.
Dieses Beispiel zeigt, wie der
mit mehrdeutigen Lösungen umgeht.
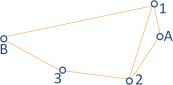
Im abgebildeten Trilaterationsnetz wurden sechs Horizontaldistanzen gemessen.
A und B sind bekannte Punkte. Es gibt genau 2 Lösungen für die Neupunkte 1 und 2 (Spiegelung an der Achse AB)
und genau 4 Lösungen für den Neupunkt 3 (zusätzliche Spiegelung an der Achse 2B).
Zunächst wird nur eine Lösung berechnet und angezeigt, wobei eine Warnung erfolgt,
dass es noch 3 zusätzliche Lösungen gibt. Mit Hilfe der Schaltfläche
kann man nun schrittweise auch die anderen Lösungen darstellen lassen.
Beachten Sie, dass schleifende Bogenschnitte (BS) berechnet wurden. In dem Beispiel greift die Vermeidung ungünstiger Schnitte nicht, weil keine Redundanz vorhanden ist und somit diese Berechnung unvermeidbar ist. Man könnte jedoch die Schnittwinkel aus dem Rechenablauf ermitteln und die unerwünschten Lösungen händisch entfernen.
Fügen Sie der Koordinatenliste eine beliebige Lösung für Punkt 3 hinzu und wiederholen Sie die Rechnung. Überzeugen Sie sich, dass jetzt nur noch eine Lösung für 1 und 2 erhalten wird. Allerdings gibt es jetzt formal eine Redundanz.
Die Ergebnisse in Form der Mediane sind in der Spalte Höhe 1 der Tabelle rechts angegeben. Die IQRs der Höhen betragen maximal 0.0021 und entsprechen den Erwartungen. (Beachten Sie, dass der IQR nicht mit der Standardabweichung zu verwechseln ist.)
Möchten Sie den klassischen Zugwiderspruch angezeigt bekommen, löschen Sie einfach entweder A oder E aus der Koordinatenliste und berechnen den Zug neu. Im ersten Fall ist das Ergebnis Z(E)=141.3795, was einem Zugwiderspruch von 0.0005 entspricht.
Dasselbe Beispiel wird auch für Höhennetze
benutzt und kann damit bearbeitet werden.
Die Ergebnisse sind allerdings nicht völlig identisch, weil
eine Ausgleichung nach kleinsten Quadraten durchführt.
Die Abweichungen in den endgültigen Höhen betragen bis zu 0.0004.
Nun betrachten wir, was passiert, wenn man einen groben Fehler einbaut. Wir verfälschen den Zenitwinkel 107.239 um 1 gon auf 108.239 und wiederholen die Berechnung.
Die Ergebnisse in Form der Mediane sind in der Spalte Höhe 2 der Tabelle rechts angegeben. Der IQR-Wert der Höhen beträgt maximal 1.026 und zeigt ein Problem an. Allerdings ändern sich die Mediane fast gar nicht, nämlich nur um maximal 0.001! Vgl. Spalte Diff. rechts. Das zeigt deutlich, wie gut die robuste Schätzung arbeitet. Der Grund ist, dass jeweils weniger als die Hälfte der Ergebnisse den verfälschten Wert benutzen. (Das muss aber nicht immer so sein!)
Schließlich probieren wir aus, wie die Ausreißererkennung arbeitet. Dem verfälschten Messwert wird die Ausreißerwahrscheinlichkeit sehr hoch zugewiesen. Alle 37 (100%) berechnete Größen werden nach der Eliminierung noch berechenbar sein, aber nur mit 39% ihrer Werte. Z.B. werden für die Neupunkthöhen jetzt nur noch je 5 Werte erhalten, vorher waren es bis zu 17. Eliminieren Sie nun den verfälschten Startwert. Alle IQRs und Spannweiten verringern sich durch die Eliminierung, maximal um 99%. Die IQRs der Neupunkthöhen verringern sich von 1.026 auf 0.0006. Ihre Mediane sind nun wieder identisch mit den Werten vor der Verfälschung.
Im Ergebnis der Berechnung werden ebene Koordinaten für alle Punkt P,Q,R,H erhalten. Die Berechnung ist sogar mehrfach möglich, weil ein Standpunkt in der Messwertliste redundant ist. (Überzeugen Sie sich, indem Sie einen beliebigen Standpunkt mit dazugehörigen Zielpunkten löschen und die Berechnung wiederholen.) Die einzelnen Ergebnisse jeder Größe stimmen aber überein, ablesbar an den IQRs oder Spannweiten, denn alle Höhen eines Dreiecks schneiden sich in einem Punkt, was hiermit für den Fall dieses Dreiecks gezeigt wäre.
Durch Klick auf die 3
in der Spalte Werte
können Sie den Rechenablauf
nachvollziehen. H wird durch Vorwärtsschnitte (VS) berechnet:
XY(H)1 = VS(XY(P)1,t(H→P)1,XY(Q)1,t(H→Q)1)
XY(H)2 = VS(XY(P)1,t(H→P)1,XY(R)1,t(H→R)1)
XY(H)3 = VS(XY(Q)1,t(H→Q)1,XY(R)1,t(H→R)1)
Die Höhenteilstücke entnimmt man der Ergebnistabelle und berechnet daraus die Produkte:
| AH=3.950 | HQ=2.686 | AH·HQ=10.61 |
| BH=6.786 | HR=1.563 | BH·HR=10.61 |
| CH=3.924 | HP=2.704 | CH·HP=10.61 |
Die Gleichheit der Produkte in der letzten Spalte folgt aus einer bekannten Gesetzmäßigkeit der Geometrie, die hier als zusätzliche Probe dient.
Laden Sie das Dreieck ABC in und berechnen Sie außerdem den Flächenschwerpunkt M2 und den Umkreismittelpunkt M3 . Überprüfen Sie dann die bekannte Tatsache, dass M2, M3 und H kollinear sind, nämlich auf der sogenannten Euler-Geraden . Tipp: Das Dreieck M2M3H sollte verschwindenden Flächeninhalt haben.
|
|
|
|