
Ein ebenes Polygon ist eine aus Geradenstücken (Seiten) zusammengesetzte ebene Kurve. Es wird durch eine Folge von Eckpunkten in einer Ebene definiert, die durch Seiten verbunden werden. Ein Polygon kann geschlossen oder offen sein. Im ersten Fall sind der letzte und der erste Eckpunkt durch eine Seite verbunden, so dass das Polygon ein ebenes Flächenstück begrenzt. Im zweiten Fall nennen wir das Polygon eine Polylinie. Die Eckpunkte werden als Koordinatenliste gegeben, die auch die Reihenfolge der Punkte definiert.
Kartesische Systeme (XY oder YX): Eine Z-Koordinate wird, wenn vorhanden, ignoriert, wobei eine Warnung erfolgt. Das bedeutet, die Punkte werden in die Horizontalebene projiziert und dort als Polygoneckpunkte aufgefasst.
Gittersysteme (Nordwert Ostwert oder Ostwert Nordwert): Höhen, soweit vorhanden, werden benutzt, um den Gittermaßstab zu berechnen. Das Polygon wird also in der horizontalen Gitterebene der mittleren Höhe aller Punkte mit gegebenen Höhen berechnet (oder der Höhe Null, wenn alle Höhen fehlen). Bei allen Längen und beim Flächeninhalt wird der Gittermaßstab berücksichtigt. Möchten Sie das Polygon in der Höhe Null berechnen, müssen alle Höhen Null gesetzt oder eliminiert werden. (Im deutschen Liegenschaftswesen werden Flächenangaben auf die Höhe Null bezogen.)
Ellipsoidische Systeme (Länge Breite oder Breite Länge) sind hier nicht direkt verwendbar, sondern erfordern eine .
Siehe auch Koordinatensystemtypen.
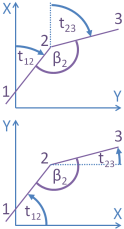
Polygonwinkel, auch Brechungswinkel genannt, liegen in Polygonzugrichtung rechts des Polygons und können beim geschlossenen Polygon entweder Innenwinkel (Zug im Uhrzeigersinn) oder Außenwinkel (Zug entgegen dem Uhrzeigersinn) sein.
Richtungswinkel, auch Azimutwinkel genannt, sind die Winkel von der X- oder Nordachse zu den Polygonseiten in Zugrichtung. Der Drehsinn des Winkels ist beim kartesischen Rechtssystem entgegen dem Uhrzeigersinn, bei allen anderen Systemtypen im Uhrzeigersinn gerichtet. Die X- oder Nordachse hat also den Richtungswinkel Null, die Y- oder Ostachse den Richtungswinkel 90° = 100 gon.
Spezielle Punkte, das sind Schwerpunkte und Kreismittelpunkte werden nur soweit möglich berechnet. Der Flächenschwerpunkt ist der Massenschwerpunkt der geschlossenen Polygonfläche. Der Seitenschwerpunkt ist der Massenschwerpunkt der Polygonseiten. Der Eckenschwerpunkt ist der Massenschwerpunkt nur der Ecken des Polygons. Um- und Inkreismittelpunkte und -radiuse werden nur bei geschlossenen Dreiecken berechnet. (Andere Polygone haben in der Regel keinen solchen Kreis.) Alle diese berechneten Koordinaten beziehen sich auf dasselbe System wie die gegebenen Eckpunktkoordinaten.
Der Flächenschwerpunkt beim überschlagenen Polygon kann weit außerhalb der Fläche liegen und ist praktisch selten sinnvoll.
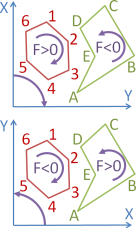
Der Flächeninhalt gibt die Größe der Polygonfläche an. Die folgende Vorzeichenregel gilt (UZS=Uhrzeigersinn):
| Flächen- | Reihenfolge der Eckpunkte | überschlagenes | |
|---|---|---|---|
| inhalt F | im UZS | gegen UZS | Polygon |
| Linkssystem | F > 0 | F < 0 | Differenzfläche |
| Rechtssystem | F < 0 | F > 0 | wird erhalten |
Der Polygondurchmesser ist der maximale Abstand aller Paare zweier Eckpunkte. Beispiel: Der Polygondurchmesser eines Rechtecks ist gleich der Diagonale.
Um den Großen Garten Dresden
wurde ein Polygon aus sieben Eckpunkten gelegt. Für diese wurden die UTM-Koordinaten
(Zone 33U) bestimmt. Die Reihenfolge wurde im Uhrzeigersinn gewählt,
dann wird die Fläche positiv erhalten und die Polygonwinkel sind Innenwinkel.
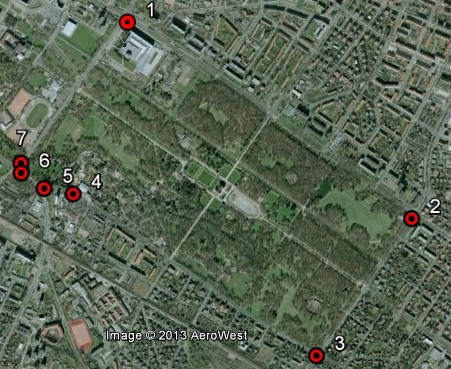
Die Polygonberechnung ergibt eine Fläche von 1811260 m² ≈ 1.8 km² und einen Umfang von 5767 m . Die längste Polygonseite ist die Seite 1-2 und hat eine Länge von 1903 m . Gegenüberliegende Seiten unterscheiden sich im Richtungswinkel um nahezu π = 180° = 200 gon, sind also etwa parallel. An den Eckpunkten 1,2,3 sind die Innenwinkel nahezu rechte Winkel. Die Eckpunkte mit dem größten Abstand sind 2 und 7, dieser beträgt 2174 m.
Die Höhen wurden in diesem Beispiel weggelassen. Deshalb beziehen sich alle Längen und die Fläche auf die Höhe Null. Der Große Garten hat eine mittlere Höhe von etwa 120 m. Wir können den Eckpunkten versuchsweise den Höhenwert 120 hinzufügen. (Einer würde ausreichen, weil als Bezugshöhe für den Gittermaßstab das Mittel aller angegebenen Höhen angesetzt wird.). Damit erhalten wir eine Fläche in Bodenhöhe von 1811328 m² . Es stellt sich heraus, dass diese 68 m² größer ist, als in Höhe Null. Dieser Höheneffekt erscheint bedeutsam. Wenn wir jedoch versuchsweise den Nordwert von Punkt 1 um 1 m erhöhen, erhalten wir eine Fläche in Höhe Null von 1812341 m². Dieser Zuwachs übersteigt den vorhergehenden Betrag um ein Mehrfaches.
Durch diese Höhenänderung vergrößern sich Längen um wenige Zentimeter. Der Umfang steigt z.B. um 0.11 m . Richtungen, Winkel und Schwerpunktkoordinaten ändern sich gar nicht. Weil die Ecken hier nicht metergenau definiert sind, ist es nicht zwingend, für diese Berechnungen Höhen zu verwenden.

Wir fügen die Mittelpunkte der beiden langen Polygonseiten als Eckpunkte hinzu und wiederholen die Berechnung. Die Polygonwinkel an diesen Punkten betragen π = 180° = 200 gon. Die Seitenlängen werden halbiert. Die anderen Werte ändert sich nicht. Teilt man jedoch das geschlossene Polygon entlang der Gerade durch die beiden Mittelpunkte in ein westliches und ein östliches Teilpolygon, durch Löschen oder Auskommentieren ('//' voranstellen) der restlichen Punkte in der Koordinatenliste , und berechnet diese Teilpolygone einzeln, so stellt man fest, dass im westlichen Teil die Längen um bis zu 1 mm kürzer und im östlichen Teil um bis zu 1 mm länger werden. Die Summe der beiden Teilflächeninhalte ist um 0.023 m² kleiner als der Flächeninhalt des Gesamtpolygons. Die Ursache liegt darin, dass bei allen Rechnungen ein konstanter Gittermaßstab verwendet wurde. Bei Teilung der Fläche ist diese Näherung besser und es werden genauere Ergebnisse erhalten.
Hier ist diese Abweichung noch vergleichsweise gering, weil Dresden nah am Zentralmeridian liegt.
und
berechnen auch einen Kreis durch drei Punkte, nämlich immer dann, wenn das geschlossene
räumliche oder ebene Polygon aus genau drei Punkten besteht. Unter
Spezielle Punkte
finden Sie den Umkreismittelpunkt
M3
und den Umkreisradius. Dasselbe geht übrigens mit dem Inkreismittelpunkt
M4
und dem Inkreisradius.
|
|
|
|