
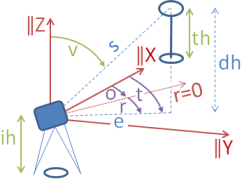
Point coordinates may be cartesian or grid coordinates and are here indiscriminately denoted as X,Y,Z . Polar measurements may be:
The combination of coordinates and measurement may be fully arbitrary . It is always computed, what is computable based on the specified quantities, in fact thoroughly . Also all measurements can be missing, while only station and target point names are given. It is tried to compute polar values from given coordinates. Polar values computed from cartesian coordinates
If different computation schemes result in the same quantities, all will be processed. The count, minimum and maximum as well as interquartile range (IQR) and common range of the obtained values per quantity are computed. If the IQR or range is small then the median should be considered as the final result, otherwise a gross error in the start values is probable. Outlier detection. In case of many different computation schemes the median is hardly falsified by a few gross errors in the input data. There is no adjustment in the traditional geodetic sense of least squares, but the results are excellently verifiable and even adjusted in the sense of a robust estimation.
Sometimes mathematically equivalent computation procedures are found. The corresponding results coincide, but are treated as separate values. This may influence the computation of the median.
If for some quantity a sufficient number of computation schemes is found, it is investigated, if the IQR or range of the obtained values can be decreased by prevention of inappropriate geodetic sections or inappropriate computations in highly acute triangles. If this case applies, the related values are discarded. The total count of discarded values is documented. In the example Inaccessible point with auxiliary triangles 1292 out of 2590 computed values have been discarded due to inappropriate section angles.
The type of system of the coordinates of the known points must be cartesian lefthanded or grid system . The distances must be corrected for instrumental errors like prism offsets, but not for the grid scale factor.
For known points at least both horizontal coordinates X,Y or Northing, Easting must be specified.
Missing coordinates and measurements are always treated as unknown, including missing instrument heights ih and target heights th ! If e.g. heights for new points are required then station and target heights must be completely specified.
Whenever possible, start values are by default also computed from other start values. This facilitates a check for gross errors also here. However, if one wants to define start values as errorfree, it is possible to suppress the recomputation of start values . This can be done for all point coordinates (only XY or only Z or XYZ), for all polar measurements (rtesvo…) or for all start quantities (XYZrte…). These options also help to keep intricate computations in perspective.
Using this one may also process . However, no instrument errors are computed and no accuracies are estimated. Therefore, we recommend to use the computation tool . You can transfer the set means obtained there directly into this .
Oftentimes the computes polar values only between points related by measurements (station and target in a station setup). More results are sometimes obtained by adding blind target points without measurements. E.g. if you want to obtain the horizontal distance between two known or computed points then they may be additionally given as station and target without measurements. This value may be used in further computations, if useful. Find such a case in the example Polar values computed from cartesian coordinates.
The total number of start values (specified point coordinates and polar measurements) is limited to 256. They must be counted as follows:
The start values are divided into two groups:
The count of start values actually used is documented.
The total computation time is limited to 90 s and the total storage consumption is limited to 128MB. Due to the laborious search for different computation schemes, in case of many start values a complete solution may take some time. The computation time can also be limited more strongly by the user. If for large scale computations this limit is eventually reached, then not all theoretically possible values are computed, but still as many as required for a reliable result in the sense of a robust estimation. A warning is issued. However, this does not mean that more computation time would really give more results.
If one of these limits is exceeded, please try to split the task. The computation time reduces also, if we suppress the recomputation of start values .
Below we sketch the universal computer algorithm. If this information is unimportant for you, please skip this section.
If a computation yields multiple solutions then calling for the solutions currently not displayed is only possible immediately after the computation. If in the meantime the computation procedure has been analysed or the outlier detection has been invoked or the result table has been sorted, the buttons for calling these solutions disappear. A recomputation puts things right.
All computed quantities are displayed in a table, sorted by type of value. Within the types of value, sorting is by (station) point names, or optionally by medians, IQRs or ranges (smallest first). Ranges are only displayed, if sorted by them, and replace the IQRs in the table. For horizontal coordinates, X and Y is always listed contiguously. When sorting by IQRs, the sum of IQRs of X and Y counts. The same applies to ranges, if sorting by ranges is selected.
Azimuths t and horizontal distances e are always displayed in one direction only, i.e. such that the two pointnames are in lexicographic order. For the opposite direction we change t by π = 180° = 200 gon. Height differences dh and slope distances s in sight and backsight may be different, if the related instrument and target heights are not equal.
The column values shows, how many values for each quantity are obtained. For position coordinates of one point the values are the same and are given only once. Possibly discarded inappropriate sections and ∄ results (not a number) are not counted. A start quantity, which in addition is computed x mal berechnet wurde, erscheint als 1+x.
The computation procedure can be retraced in detail. If we do not need this feature, skip this section. For a desired quantity click on the value(s) in column values to get the detailed documentation of the computation procedure and the individual results.
In addition to the symbols for the measurements listed in the the following abbreviations are used. The table shows, which result a computation step may produce.
| Symbol | computation step | unique | ambiguous | bad section | not a number |
|---|---|---|---|---|---|
| Rec2Pol/ Pol2Rec | coordinate conversion cartesian⇔polar | X | |||
| AA | arcs-intersection | X | X | X | |
| LA | straightline-arc-intersection | X | X | X | X |
| LL | straightlines-intersection | X | X | X | |
| RE | resection | X | X | X |
Assume that the angle unit is gon . A computation step is documented like:
t(P1→3)7 = r(3°2→P1) + o(3°2)3 ± 200 = 69.965792398379
This can be understood as follows: The 7th value of the azimuth t from point P1 to point 3 is computed from the given horizontal angle r (index missing → start value) measured during the second setup on the station point 3 to point P1 and the 3rd computed value of the orientation angle o for the second setup on the station point 3 . The result is 69.965792398379 in the chosen unit of angle Grad . If there is only on setup per station, the setup counter behind the station point name is omitted. Or e.g.:
XY(2)9 = LL(XY(1)5,t(1→2)2,XY(Q3),t(2→Q3)4) = ∄
This can be understood as follows: The 9th computed values of the positional coordinates XY of point 2 are computed by straightlines-intersection (LL) from the 5th values of the coordinates XY of point 1 , from the 2nd computed value of the azimuth t from point 1 to point 2 , from the given values of the coordinates XY (index missing → start values) of point Q3 and from the 4th computed value of the azimuth t from point 2 to point Q3 . The result is ∄ , (not a number), because due to gross errors in the start values no real section of the rays exists.
In the documentation of the computation procedure also the values discarded due to inappropriate sections are displayed.
If a sufficient number of values per computable quantity is obtained, it can be tried to detect outliers in the start values (coordinates and measurements). Below the result table a button appears. If we click it, the results are analysed for outliers.
This outlier detection shows, what would happen, if a start value would be eliminated and the computation would be repeated. This would give less results, but the remaining results would be unchanged. As a consequence, for some results we would often get smaller IQRs and ranges. An outlier is identified by a drastic reduction of such values. Note that for outlier detection the ranges prior to the prevention of inappropriate sections are the decisive factors.
The outlier detection creates a table with the following information per start value:
| still computable quantities |
It is possible that after elimination of a start value some quantities are no longer computable. The table shows, how many percent of the quantities are still computable. Start quantities, for which no second value can be computed anymore, are counted as no longer computable here. 100% means: After elimination all quantities can still be computed, at least once. |
|---|---|
| still computable values |
After elimination of a start value not all values are still computable. The table shows the percentage of the values still computable. If this number is small then this start value is very important for a reliable solution and an elimination is questionable. |
| smaller ranges |
The table shows the percentage of the ranges getting smaller after elimination of a start value. If this number is large then this start value is probably an outlier. |
| maximum reduction |
The table shows the size of the maximum relative reduction of a range in percent. If this number is large then this start value is probably an outlier. |
| outlier probability |
The probability, that a start value is an outlier, is rated. Note that even if high outlier probability is assigned to many start values, this does not mean that all of them are outliers. It can well be only one of them. |
If some start quantities are missing in the table, then they cannot be investigated for outliers due to small redundancy. If the total redundancy is small, the outlier detection fails sometimes. An error message is generated.
Now a start value to be eliminated can be selected (1st column of the outlier table). A candidate is pre-selected. Clicking the button redisplays the results remaining after the selected start value has been eliminated. (The actual computation is not repeated.) Although an eliminated start value continues to appear in the list of known points or input measurements, it is not used anymore. If the redundancy is still sufficiently large, a renewed outlier detection can be requested, etc.
An application of the outlier detection can be found in the example Trigonometric levelling line.
The points of the penalty area of a football pitch 1,2,3,4,5,6 must be staked out by a tacheometer, which is set up at the corner points A,B of the pitch. The instrument heights are 1.42 m at A and 1.55 m at B. At the target points a stake out reflector of height 0.15 m is used. The azimuths t, slope distances s and zenith angles v of the six points to be staked out are desired.
First of all, we define a coordinate system, favorably a lefthanded cartesian system YXZ and determine the cartesian coordinates of all points in this system in metre. For example, as can be seen from the figure below, the coordinate X of point 6 is 75.00/2-7.32/2-5.50-11.00=17.34 and the coordinate y is 5.50+11.00=16.50. Heights are all set to 0.00. Now we set up the .
The consists of two stations A and B. The station rows must contain the instrument heights 1.42 and 1.55. Since all target points have identical reflector heights 0.15, they can be specified by the default target height (default value of the target height) in the station row and omitted in the target rows. Then the target rows consist only of the target point names. The format selected for the empty columns is irrelevant, may be e.g. ''code / unused''.
The processing engine searches for computable quantities and finds height differences dh , horizontal distances e, slope distances s , azimuths t and zenith angles v , though only for the lines of sight. Nothing is computed between the target points among themselves. If e.g. the distance between 1 and 3 is desired then a further station 1 with target point 3 ( blind target point ) should be specified, or vice versa.
Moreover, we only get the azimuths from target to station here. This is because azimuths and horizonal distances are always given such that the two pointnames are in lexicographic order. Digits are prior ranking. Therefore, the azimuths must be changed by 200 grads. In order to get azimuths in sighting direction nonetheless, it is possible to rename the points, e.g. from 1 to P1 etc. Another possibility is to enforce the output of horizontal angles, which are always given from station to target. For this purpose, each station row must be augmented by the orientation angle 0.
Finally, after reasonable rounding, we obtain the following polar stakeout values in metres and grads:
| s | t | v | s | t | v | |||
|---|---|---|---|---|---|---|---|---|
| A→1 | 47.000 | 7.470 | 101.720 | B→1 | 28.903 | 187.797 | 103.085 | |
| A→2 | 28.897 | 12.203 | 102.799 | B→2 | 47.004 | 192.530 | 101.896 | |
| A→3 | 39.101 | 18.165 | 102.068 | B→3 | 39.105 | 181.835 | 102.280 | |
| A→4 | 59.988 | 17.743 | 101.348 | B→4 | 23.977 | 151.580 | 103.719 | |
| A→5 | 42.590 | 31.390 | 101.899 | B→5 | 42.594 | 168.610 | 102.093 | |
| A→6 | 23.970 | 48.420 | 103.375 | B→6 | 59.991 | 182.257 | 101.486 |
If prefered, also other stakeout values can be taken from the result table, e.g. e or dh.
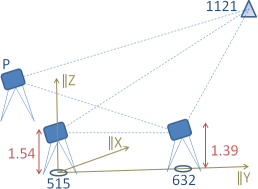
An inaccessible point 1121 was measured from three tacheometry stations 515,632,P. The height of point 515 amounts to 107.483 m, the instrument height is here 1.54 m. The height of point 632 amounts to 107.832 m, the instrument height is here 1.39 m. The height of the auxiliary point P is unknown. An arbitrary value can be assigned to the instrument height of P, say 0.00 m. The target heights equal the instrument heights on the same point, because matching instruments and reflectors have been used. The inaccessible point 1121 was directly sighted without distance measurement, such that the corresponding target height equals 0.00 m. The height of point 1121 can be computed in both auxiliary triangles 515,632,1121 and P,632,1121. The measurement values are:
| station | target | horiz. | zenith | slope |
|---|---|---|---|---|
| point | point | angle | angle | distance |
| name | name | [grads] | [grads] | [m] |
| 515 | 1121 | 149.846 | 91.886 | --- |
| 632 | 187.807 | 99.991 | 952.233 | |
| 632 | 515 | 260.607 | 100.018 | 952.233 |
| P | 260.740 | 100.086 | 941.461 | |
| 1121 | 314.405 | 89.258 | --- | |
| P | 1121 | 28.449 | 91.684 | --- |
| 632 | 66.940 | 99.923 | 941.461 |
Since pure levelling benchmarks are not supported, it is necessary to introduce a local coordinate system, favourably a cartesian lefthanded system XYZ. First of all we need the horizontal distance 515→632. For this aim, a simple computation using the can be run, very much like in the preceeding example. The result is 952.233, equal to the slope distance of 515→632, because both points have nearly the same height. We define X515=1000, Y515=1000, X632=1000, Y632=1952.233. As a result, the defined Y-axis is parallel to the projection of 515→632 onto the horizontal plane. Now we set up the and the . For the unmeasured distances to the inaccessible point 1121 we put 0. The same effect would have a negative or non-numerical value. An alternative notation of an unmeasured value can employ the '';;'' method, see Tabular data records.
As a result, 49 quantities with totally 2590 different values are obtained. 1292 values of them are discarded due to inappropriate section angles. For the height Z of the inaccessible point 1121 no less than 52 different solutions are computed. For the IQR value we obtain 7 mm , which is convincing, the median amounts to 2201,111 m.
The following should be noted:
The same example is also used for
Vertical networks
and may be computed. However, the results are not fully identical because
computes a least squares adjustment, where also the standard deviation of
1.4 mm is obtained.
The deviation in the final height of the inaccessible point
1121 amounts to only 0.43 mm.
This example shows how the
deals with ambiguous solutions.
In the displayed trilateration network six horizontal distances have been measured. A and B are known points.
There are exactly 2 solutions for the unknown points 1 and 2 (reflection with respect to axis AB)
and exactly 4 solutions for the unknown point 3 (additional reflection with respect to axis 2B).
Firstly, only one solution is computed and displayed, while a warning is issued, that there are 3 extra solutions.
By means of the button
all the other solutions are displayed step by step.
Note that arcs-intersections (AA) with bad section angles have been computed. In this example the prevention of inappropriate sections is not effective, because there is no redundancy. Hence, this computation is unavoidable. However, we could inquire the section angles via the Computation procedure and reject the undesired solutions manually.
Augment the coordinate list by an arbitrary solution for point 3 and repeat the computation. See for yourself that only one solution remains for points 1 and 2. However, there is formally a redundancy now.
The results in terms of the medians are given in the column Height 1 of the table at the right. The IQRs of the heights amount ot a maximum of 0.0021 and meet the expectations. (Note that the IQR is not to be confused with the @standard deviation@.)
If we want to get the classical levelling misclosure, delete either A or E in the coordinate list and re-compute. In the first case the result is Z(E)=141.3795, which corresponds to a levelling misclosure of 0.0005 .
The same example is also used for
Vertical networks
and may be computed. However, the results are not fully identical because
computes a least squares adjustment.
The deviations in the final heights amount up to 0.0004.
Now we observe, what happens, if we implement a gross error . We falsify the zenith angle 107.239 by 1 gon getting 108.239 and repeat the computation.
The results in terms of the medians are given in the column Height 2 of the table at the right. The IQR value of the heights amount ot a maximum of 1.026 and indicate a problem. However, the medians are almost unchanged, they change by no more than 0.001! See column Diff. at the right. This shows clearly, how well the robust estimation works. The reason is that less than half of the results use the falsified value. (However, this must not always be so.)
Finally, we test the outlier detection . The outlier probability very high is assigned to the falsified value. All 37 (100%) computed quantities are still computable after elimination, but only with 39% of their values. E.g. for the computed height of the new points we only get 5 values, previously up to 17. Now eliminate the falsified start value. All IQRs and ranges are decreased by the elimination, by up to 99%. The IQRs decrease from 1.026 to 0.0006. The medians are now again identical to the values before the falsification.
As results of the computation we obtain planar coordinates for all points P,Q,R,H. The computation can be performed even multiple times because one station in the measurement list is redundant. (Prove this by deleting an arbitrary station with the associated targets and repeating the computation.) However, the individual results for each quantity coincide, which can be verified by the IQRs or ranges, because all altitudes intersect in a common point, which is demonstrated herewith for the case at hand.
By clicking on 3
in the column values
you can retrace of the
computation procedure
. H is computed by straightlines-intersections (LL):
XY(H)1 = LL(XY(P)1,t(H→P)1,XY(Q)1,t(H→Q)1)
XY(H)2 = LL(XY(P)1,t(H→P)1,XY(R)1,t(H→R)1)
XY(H)3 = LL(XY(Q)1,t(H→Q)1,XY(R)1,t(H→R)1)
The segments of the altitudes can be taken from the result table, and the following products can be computed:
| AH=3.950 | HQ=2.686 | AH·HQ=10.61 |
| BH=6.786 | HR=1.563 | BH·HR=10.61 |
| CH=3.924 | HP=2.704 | CH·HP=10.61 |
The equality of the products in the trailing column follows from a well-known law of geometry, which is used here as an additional check.
Load the triangle ABC into and compute the barycentre of area M2 and the centre of circumscribed circle M3 . Now, check the well-known fact, that M2, M3 and H are collinear, i.e. namely located on the Euler line . Tip: The triangle M2M3H should have vanishing area.
|
|
|
|