Seiteninhalt

Näherungsweise Korrektur in kleinen Punktgebieten Andere metrische Werte und Maßstäbe Punktmaßstabsfaktoren Linienmaßstabsfaktoren Punkte auf dem 51°-Parallelkreis In der Bibliothek

Der Punktmaßstabsfaktor von Gittersystemen an den Punkten von und der Linienmaßstabsfaktor entlang der Linien zwischen aufeinanderfolgenden Punkten solcher Listen werden berechnet.

≡ START Erste Schritte English

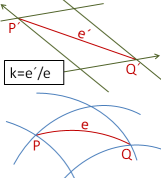
Gittersysteme (Systemtyp: Nordwert Ostwert Höhe oder Ostwert Nordwert Höhe) basieren auf einer lokalen Verebnung des gekrümmten Rotationsellipsoids mittels Gaußscher Abbildung (= Transversale Mercator-Abbildung auf dem Ellipsoid). Wegen der unvermeidbaren Verzerrungen stimmt die Gitterkoordinateneinheit nicht mit der metrischen Längeneinheit überein. Dieses wird mit einem Gittermaßstabsfaktor k korrigiert. Es gilt k > 1, wenn Gitterdistanzen (=Kartendistanzen) e´ länger sind, als Bodendistanzen (=Naturdistanzen) e, und k < 1, wenn dies umgekehrt ist.

Die korrekte Berechnung und Berücksichtigung von k setzt voraus, dass die für die Koordinatensystemparameter korrekt sind. Vorsicht ist geboten, wenn Sie mit gekürzten Koordinaten arbeiten. Die Einstellungen falscher Ostwert und falscher Nordwert müssen dann um denselben Betrag geändert werden! Siehe hierzu auch das GPS-Referenzpunkt der HTW Dresden.

≡ START Erste Schritte English Näherungsweise Korrektur in kleinen Punktgebieten

Resultierend aus der Winkeltreue der Gaußschen Abbildung ist in einem kleinen Punktgebiet der Gittermaßstabsfaktor k etwa konstant und wird näherungsweise automatisch wie folgt berechnet:

E	= mittlerer Ostwert im Punktgebiet
h	= mittlere ellips. Höhe im Punktgebiet
Eo	= falscher Ostwert , eingestellt ist inital 500000.
ko	= Maßstabsf. am Zentralmeridian , eingestellt ist initial 0.9996.
R	= Radius der Gaußschen Schmiegekugel

k=ko+	(E-Eo)²	−	h
	2koR²		R

Die mittlere Höhe h wird nur aus den Punkten berechnet, für die Höhen angegeben sind. Sie wird mit 0.000 angenommen, wenn keinerlei Höhen gegeben sind, wobei eine Warnung erfolgt. Im Flachland ist der Einfluss der Höhe gering. Er beträgt bis 15 ppm bei einer Höhe bis 100 m.

Diese Korrektur wird von IN DUBIO PRO GEO bei allen Berechnungen mit Gitterkoordinaten verwendet, außer bei . Dieses Rechenwerkzeug dient zur wesentlich genaueren Bestimmung der Korrektur. Dazu mehr in den folgenden Abschnitten.

In den Informationen zu einer Gitterkoordinatenliste wird der berechnete Maßstabsfaktor im Punktgebiet ausgewiesen. Ist das Punktgebiet groß, werden statt dessen die Extremwerte des Maßstabsfaktors im Punktgebiet ausgewiesen. Das gilt als Warnung, dass die Berechnung ungenau sein könnte, denn verwendet wird trotzdem nur ein Maßstabsfaktor pro Gitterkoordinatenliste, nämlich der Mittelwert.

Sind die Punkte über ein sehr großes Gebiet verteilt, so ist der Maßstabsfaktors nicht repräsentativ für das ganze Punktgebiet. Das passiert normalerweise vor allem bei großer Ost-West-Ausdehnung oder vertikaler Ausdehnung des Gebietes. Wenn möglich, sollte man in diesem Fall die Liste filtern, so dass Punkte außerhalb des interessierenden Gebiets abgeschnitten werden.

In den kann vereinbart werden, auf wieviele Ziffern k im Punktgebiet übereinstimmen muss, damit eine Berechnung erfolgt. Standard ist 3 Nachkommastellen. Dann würde z.B. min(k)=0.999267, max(k)=0.999783 eine Berechnung erlauben, andernfalls erhält man eine Fehlermeldung.

≡ START Erste Schritte English Andere metrische Werte und Maßstäbe

Bei Berechnungen mit Gitterkoordinaten wird vorausgesetzt, dass alle anderen metrischen Werte und Maßstäbe nicht mit dem Gittermaßstab behaftet sind. Das sind folgende Größen:

Rechenwerkzeug	nicht mit dem Gittermaßstab behaftet
	Rasterweiten und Kantenlängen
	Seitenlängen, Polygonumfang, Flächeninhalt, Radien von Kreisen
	Translationsparameter, Transformationmaßstäbe
	Radius der ausgleichenden Kugel, Halbachsen des ausgleichenden Ellipsoids und Hyperboloids etc.
	Horizontal- und Schrägdistanzen

Möchten Sie dennoch solche Daten im Gittermaßstab eingeben, hilft folgender Trick:
Messwertlisten mit Distanzen etc. im Gittermaßstab .

≡ START Erste Schritte English Punktmaßstabsfaktoren

Das Rechenwerkzeug dient zur wesentlich genaueren Bestimmung der Maßstabsfaktoren mittels einer ausreichend langen Reihenentwicklung. Diese erreichen ihre hohe Genauigkeit jedoch nur in einer sehr kleine Umgebung eines Punktes. Bei gegebener Gitter- oder ellipsoidischer Koordinatenliste wird zu jedem Punkt ein zugehöriger Maßstabsfaktor berechnet. Dieser Faktor bezieht sich auf Horizontaldistanzen in der Höhe des Punktes.

Für die gegebene Koordinatenliste wird grob abgeschätzt, wie groß der Fehler der Reihenentwicklung maximal sein kann.

≡ START Erste Schritte English Linienmaßstabsfaktoren

Zwischen allen aufeinanderfolgenden Punkten der Koordinatenliste wird das Verhältnis der Länge der geodätischen Linie (Bodendistanzen) zu ihrem Bild im Gitterraum (Gitterdistanz) berechnet. Hierfür kommt eine ausreichend genaue Quadraturformel zum Einsatz. Jeder erhaltene Linienmaßstabsfaktor bezieht sich auf Horizontaldistanzen in der mittleren Höhe der zugehörigen Linie.

Für die gegebene Koordinatenliste wird grob abgeschätzt, wie groß der Fehler der Quadraturformel maximal sein kann.

≡ START Erste Schritte English Punkte auf dem 51°-Parallelkreis

Der UTM-Gittermaßstabsfaktor für gleichabständige Punkte auf dem 51°-Parallelkreis wird berechnet. Der Punktabstand beträgt 0.2° ≈ 14 km. Die Punktmaßstabsfaktoren variieren zwischen 0.9996 und 1.000144. Die Linienmaßstabsfaktoren variieren zwischen 0.9996 und 1.000109.

und Rechnen   Beim Laden werden Projekteinstellungen angepasst.

Schon gewusst? Auf der Startseite durchsuchen Sie IN DUBIO PRO GEO mit der Google Suchmaschine.

≡ START Erste Schritte English