Durch gegebene Stützpunkte im 3D-Raum wird eine ausgleichende (d.h. bestanpassende) Fläche (Ebene, Kugel, Ellipsoid oder allgemeine Quadrik) berechnet. Auch eine Ebene durch 3 Punkte, eine Kugel durch 4 Punkte usw. kann berechnet werden. Weitere Punkte können auf die Flächen projiziert werden.

≡ START Erste Schritte English Stützpunkte

Ebene	3
Kugel	4
Ellipsoid/ ellipt. Hyperboloid	6
allg. Quadrik	9

Zunächst sind Stützpunkte anzugeben, durch die die Fläche verlaufen soll, eventuell nur näherungsweise. Alle diese Punkte müssen 3D-Punkte sein, also drei gegebene Koordinaten besitzen. Diese Koordinaten werden über eingegeben. In der rechten Tabelle ist für jede Flächenart die Mindestanzahl von Stützpunkten angegeben. Wenige spezielle Konfigurationen von Stützpunkten können zu singulären Gleichungssystemen führen und sind unzulässig.

≡ START Erste Schritte English Flächen, Flächenparameter und Flächengleichungen

Als Ergebnis erhalten Sie für die gewünschte Fläche zunächst die Flächengleichung, in der Sie die Parameter der Fläche ablesen können, die ihre Größe, Form, Lage und Ausrichtung definieren.

Ebene: (v_X, v_Y, v_Z)^T ist ein Einheitsvektor senkrecht auf der Ebene (der sogenannte Normaleneinheitsvektor), der vom Koordinatenursprung weg zeigt. w>0 ist der Abstand des Koordinatenursprungs von der Ebene:

v_X · X + v_Y · Y + v_Z · Z = w

Kugel: X_o, Y_o, Z_o sind die Koordinaten des Mittelpunkts, R ist der Radius der Kugel:

(X_o - X)² + (Y_o - Y)² + (Z_o - Z)² = R²

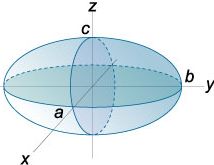
Dreiachsiges Ellipsoid / elliptisches Hyperboloid: X_o, Y_o, Z_o sind die Koordinaten des Mittelpunkts der Figur, a,b,c > 0 sind die Formparameter der Fläche. Beim Ellipsoid sind das die Halbachsen. Auch beim elliptischen Hyperboloid werden diese manchmal Halbachsen genannt. Die Symmetrieachsen und -ebenen der Fläche verlaufen durch den Mittelpunkt und liegen parallel zu den Koordinatenachsen und -ebenen:

±	(Xo - X)²	±	(Yo - Y)²	±	(Zo - Z)²	= 1
	a²		b²		c²

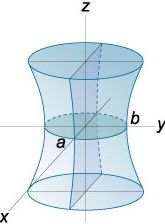
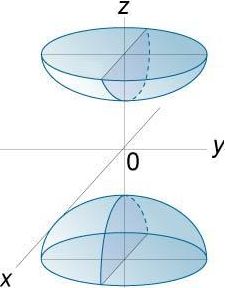
Die Art der Fläche hängt von den Vorzeichen der Brüche in dieser Gleichung ab:

• 3× plus ⇒ Ellipsoid,
• 2× plus, 1× minus ⇒ einflächiges elliptisches Hyperboloid,
• 1× plus, 2× minus ⇒ zweiflächiges elliptisches Hyperboloid,
• 3× minus ist nicht möglich.

Allgemeine Quadrik: Dieser Flächentyp ist nichts anderes als ein dreiachsiges Ellipsoid oder elliptisches Hyperboloid in schräger (nicht achsenparalleler) Lage:

Xo - X Yo - Y Zo - Z . uXX uXY uXZ uXY uYY uYZ uXZ uYZ uZZ . Xo - X Yo - Y Zo - Z

=1

X_o, Y_o, Z_o sind die Koordinaten des Mittelpunkts der Figur. Alles andere wird von den Eigenwerten und Eigenvektoren des Matrixfaktors U bestimmt. Die Vorzeichen der Eigenwerte bestimmen den Flächentyp nach derselben Regel, wie oben. Die Halbachsen sind die Eigenwerte hoch -0.5. Die Eigenvektoren sind parallel zu den Achsen der Quadrik.

≡ START Erste Schritte English Algebraische Ausgleichung

Sind mehr Stützpunkte vorhanden, als zur eindeutigen Bestimmung der Fläche erforderlich sind (Redundanz, Tabelle), erfolgt die Ausgleichung durch die Methode der gewichteten kleinsten Quadrate. Bei der Algebraischen Ausgleichung werden die Konstanten auf der rechten Seite der Flächengleichung w, R² oder 1 als gleichgewichtige Beobachtungen angesehen und ''verbessert''. Möglicherweise gegebene Standardabweichungen oder Gewichte werden nicht verwendet.

≡ START Erste Schritte English Stochastische Ausgleichung

In diesem Fall werden Genauigkeitsmaße für die Koordinaten der Stützpunkte benötigt, entweder als Standardabweichungen σ oder als Gewichte p. Im ersten Fall werden Gewichte berechnet entsprechend p=1/σ². Im Unterschied zur Algebraischen Ausgleichung sind hier die mit Genauigkeitsmaßen versehenen Koordinaten der Stützpunkte die Beobachtungen. Koordinaten ohne Genauigkeitsmaß gelten als fehlerfrei und erzeugen eine Bedingungsgleichung. Sind mehr fehlerfreie Koordinaten als Flächenparameter vorhanden, ist die Berechnung nicht möglich.

≡ START Erste Schritte English Zu projizierende Punkte

Optional können Punkte angegeben werden, die auf die berechnete Fläche projiziert werden sollen. Die Koordinaten dieser Punkte werden über eingegeben. Systemtyp und Spaltenformat müssen mit den Einstellungen der Stützstellen übereinstimmen. Zwei verschiedene Modi werden unterstützt:

2D-Punkt (zwei gegebene Koordinaten):

Es wird versucht, die dritte Koordinate so zu finden, dass der Punkt in der Fläche liegt (Projektion entlang der dritten Achse). Sollte es keinen solchen Punkt geben, wird ∄ erhalten. Sollte es zwei geben, wird derjenige Punkt erhalten, der näher an den Stützpunkten liegt.

3D-Punkt (drei gegebene Koordinaten):

Der in der Fläche nächstgelegene Punkt wird berechnet (senkrechte Projektion auf die Fläche). Für jeden Punkt wird der Projektionsvektor zum Bild in der Fläche angegeben, woraus auch der Abstand berechnet werden kann.

Wenn die zu projizierenden Punkte weit von den Stützpunkten entfernt liegen, ist die Genauigkeit oft schlecht wegen der ungünstigen Fehlerfortpflanzung der Extrapolation.

Es ist möglich, dass Stützpunkte und zu projizierende Punkte dieselben Namen haben. Unvermeidlich wird dieser Fall eintreten, wenn das Spaltenformat ''Koordinaten'' gewählt wurde. Um Verwechslungen zu vermeiden, wird diese Option hier nicht empfohlen.

Im Fall von zu projizierenden 3D-Punkten haben der zu projizierende Punkt und der in der Fläche nächstgelegene Punkt dieselben Namen. Falls das unerwünscht ist, kann an die Namen projizierter Punkte ein Suffix angehängt werden, um diese von den zu projizierenden Punkten zu unterscheiden.

≡ START Erste Schritte English Auf der Leinwand

Auf der Leinwand werden alle Stützpunkte und projizierte Punkte sowie zu projizierende Punkte im Grundriss dargestellt. Für jeden Punkt wird nur die letzte gültige Koordinatenlösung dargestellt. Haben projizierte Punkte also keinen Suffix, so werden zu projizierende Punkte nicht dargestellt. Im Spaltenformat ''Koordinaten'' werden ebenfalls manche Punkte nicht auf der Leinwand erscheinen können.

≡ START Erste Schritte English Verwendung eines Gittersystems

ist z.Z. noch nicht möglich. Bitte kartesisches System verwenden.

≡ START Erste Schritte English Geländemodellapproximation und -interpolation
im Großen Garten Dresden

Im Dresdner Großen Garten wurden folgende Geländepunkte gemessen:

  Ostw. [m] Nordw. [m] Höhe [m]
1 413736      5653962      122
2 414006      5654264      123
3 414145      5654626      117
4 413496      5654915      121
5 413035      5655364      114
6 412418      5654935      116
7 413134      5654353      121
8 413163      5654817      115
9 413678      5654471      121

Obwohl diese Koordinaten sich auf die UTM Zone 33U beziehen, arbeiten wir mit einem kartesischen System, solange Gittersysteme in noch nicht unterstützt werden. Wegen der geringen Genauigkeit der Lagekoordinaten spielt ein Gittermaßstabsfaktor sowieso keine Rolle.

Das mittlere Geländegefälle soll bestimmt werden, indem eine ausgleichende Ebene durch diese 9 Punkte berechnet wird. Auf dieser Ebene sollen Rasterpunkte mit einer Rasterweite 100 m × 100 m berechnet werden. (Tipp: )

und Rechnen

Die erhaltene Ebene kann durch die Gleichung

0.0057072740260338 · X -0.00092455626269208 · Y + 0.99998328596978 · Z = 32009.200056141

beschrieben werden, aus der man sofort den Neigungswinkel abliest:

arccos(0.999983286) = 0.331° = 19.9`

Außerdem erhält man den Richtungswinkel der Falllinie:

arctan(-0.000925/0.005707) = 350.8° = 389.8 gon

Das stärkste Gefälle finden wir etwa in nördlicher Richtung.

≡ START Erste Schritte English Ebene durch drei Punkte, Kugel durch vier Punkte

berechnet auch eine Ebene durch drei Punkte oder eine Kugel durch vier Punkte. Gewichte sind dann egal, können auch fehlen. Wenn Sie die Abstände weiterer Punkte von der Fläche und/oder ihre Projektionen auf die Fläche benötigen, geben Sie diese als zu projizierende Punkte an. Die Abstände berechnen Sie als Längen der Differenzvektoren.

Eine andere Lösung für die Kugel durch vier Punkte ist mittels und dem Kugelschnitt mit vier Pseudodistanzen möglich. Man gibt die vier Punkte als Mittelpunkte von vier Kugeln mit identischen Pseudodistanzen an, am einfachsten mit 0;0;0;0. Der Radius der gesuchten Kugel ist die sich ergebende viermal identische Distanz. Der Mittelpunkt der gesuchten Kugel ist der sich ergebende Schnittpunkt der vier Kugeln. Der praktische Vorteil dieser Methode ist, dass dieser Mittelpunkt direkt in eine Koordinatenliste geladen werden kann. (Rechnerisch ergeben sich allerdings zwei identische Schnittpunkte, einer mit ''negativem'' Radius gleichen Betrags, der verworfen werden kann.)

Schon gewusst? Sollten Sie Javascript deaktiviert haben, nutzen Sie immer noch fast alle Funktionen. IN DUBIO PRO GEO verzichtet auf Cookies.

≡ START Erste Schritte English

Ausgleichungslehrbücher