Seiteninhalt

Aufgabe Hintergrund Lösung durch Polygonzugberechnung Lösung mit Universalrechner Erweiterte Lösung Lösung mit grobem Fehler in einem bekannten Punkt In der Bibliothek

Die Tutorien erläutern die Funktion von IN DUBIO PRO GEO anhand von Praxisbeispielen. Die Lösungen zu den Aufgaben sind mittels vorausgefüllter Formulare nachvollziehbar. In den Auswahlfeldern stehen nicht alle Optionen zur Verfügung. Die Formulare lassen sich mit der Schaltfläche absenden und so die Ergebnisse betrachten. Um das zu ersparen, sind die Ergebnisse im Tutorium auszugsweise dargestellt. Die wesentlichen Zwischen- und Endergebnisse sind durch goldfarbene Boxen hervorgehoben. Die Lösungen sind in weiteren goldfarbenen Boxen kommentiert. Ihre eigene Ausgabe unterscheidet sich möglicherweise in der Darstellung etwas, abhängig von Ihren .

≡ START Anleitung English Aufgabe

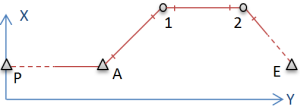
Der abgebildete unvollständig angeschlos-
sene Polygonzug wurde gemessen. Folgende Anschlusspunkte sind gegeben:

Punkt  X [m]     Y [m]      Z [m]
P    100.004      0.002    
A     99.996    100.004     99.998
E     99.984    249.993    130.014

Folgende Messwerte wurden auf den drei Standpunkten A,1,2 erhalten:

               Instrumentenhöhe/ Horizontal-    Zenit-       Schräg-
               Zielhöhe [m]      richtung [gon] winkel [gon] distanz [m] 
Standpunkt A    1.69
 Rückblick P                     299.9993
 Vorblick  1    1.71              50.0006       91.0568       71.410

Standpunkt 1    1.71
 Rückblick A    1.68             250.0017
 Vorblick  2    1.69             100.0006

Standpunkt 2    1.69
 Rückblick 1    1.71             300.0004       112.5667      50.989
 Vorblick  E    1.69             149.9989        91.0576      71.414

Berechnen Sie die Neupunkte 1 und 2.

≡ START Anleitung English Hintergrund

Diese Koordinaten und Messwerte wurden simuliert auf der Basis der wahren Koordinaten

Punkt   X [m]     Y [m]      Z [m]
P      100.000     0.000   
A      100.000   100.000   100.000
1      150.000   150.000   110.000
2      150.000   200.000   120.000
E      100.000   250.000   130.000

und addierten simulierten Koordinaten- und Messabweichungen, um die Wirkung von zu demonstrieren. Schrägdistanzen und Zenitwinkel aus Sicht und Gegensicht zwischen A und 1 sowie zwischen 1 und 2 wurden vorher gemittelt.

≡ START Anleitung English Lösung durch Polygonzugberechnung

IN DUBIO PRO GEO Tachymetrie : Polygonzüge

Aus Punktkoordinaten und polaren Messwerten wird versucht, einen klassischen Polygonzug mit Verteilung der Widersprüche zu berechnen. In beliebigen Messwerten wird der längstmögliche Polygonzug erkannt. Was auf irgendeine Art sinnvoll auswertbar ist, wird ausgewertet.

Winkeleinheit Gon [-200...200]    Notiz

Bekannte Punkte	Punktnamen und Koordinaten
Systemtyp: X Y Z linkshändig Spaltenformat: Punktname Koordinaten	P 100.004 0.002 // Höhe fehlt A 99.996 100.004 99.998 E 99.984 249.993 130.014 IN DUBIO PRO GEO behandelt Fehlendes als unbekannt. Was sich dann nicht berechnen lässt, wird nicht berechnet

Punktnamen (Spalte 1) und Messwerte (Spalte 2…5)

zweite Spalte: Instrumentenhöhe dritte Spalte: Code / nicht benutzt vierte Spalte: Code / nicht benutzt fünfte Spalte: Code / nicht benutzt Format Zielpunktzeile zweite Spalte: Horizontalrichtung dritte Spalte: Zielhöhe vierte Spalte: Zenitwinkel fünfte Spalte: Schrägdistanz

A 1.69 P 299.9993 1 50.0006 1.71 91.0568 71.410 ~~~~~~~~~~~~~ Trennzeile ~~~~~~~~~~~~~ 1 1.71 A 250.0017 1.68 2 100.0006 1.69 ~~~~~~~~~~~~~ Trennzeile ~~~~~~~~~~~~~ 2 1.69 1 300.0004 1.71 112.5667 50.989 E 149.9989 1.69 91.0576 71.414 Am Besten wird die Reihenfolge der polaren Messwerte so gewählt, dass keine Lücken durch fehlende Messwerte entstehen. Weil P keine definierte Höhe hat, ist eine Zielhöhe sinnlos. In der Originalreihenfolge der Aufgabe hätte hierfür ein Platzhalter eingefügt werden müssen, also irgendeine Zeichenkette, die nicht als Zahl interpretierbar ist. Das erzeugt eine Warnung, die ignoriert werden kann. Alternativ könnte man irgendeine Zahl eintragen. Das ist in diesem Fall unschädlich, weil diese wegen fehlender Höhe von P ohnehin nicht für Berechnungen brauchbar ist.

Gemessene Richtungen nicht verbessern (nur Widersprüche ausweisen)
Distanzmaßstab an Koordinaten bekannter Punkte anpassen
Koordinatenliste erzeugen nein danke

Probieren Sie es aus: liefert in Auszügen Folgendes:

IN DUBIO PRO GEO Tachymetrie : Polygonzüge

Unvollständig angeschloss. Polygonzug

3 benutzte bekannte Punkte: lokal, kartesisches Linkssystem

Tipp: Sie können Zahlen nicht nur mit Dezimalkomma eingeben, sondern erhalten sie auf Wunsch auch so. (Ausgabe­dezimal­trenn­zeichen in auf Komma setzen)

Punktname	X	Y	Z
P	100.004	0.002
A	99.996	100.004	99.998
E	99.984	249.993	130.014

Eingabe-Messwerte

Symbole:

o	Orientierungswinkel	r	Horizontalrichtung	e	Horizontaldistanz
ih	Instrumentenhöhe	t	Richtungswinkel	s	Schrägdistanz
th	Zielhöhe	v	Zenitwinkel	dh	Höhendifferenz

In den sucht IN DUBIO PRO GEO sucht nach dem längstmöglichen Polygonzug, egal in welcher Reihenfolge die Eingabe-Messwerten gegeben sind.

StandPname	ih
A	1.69

ZielPname	r	th	v	s
P	299.9993
1	50.0006	1.71	91.05680	71.41

StandPname	ih
1	1.71

ZielPname	r	th	v	s
A	250.0017	1.68
2	100.0006	1.69

StandPname	ih
2	1.69

ZielPname	r	th	v	s
1	300.0004	1.71	112.5667	50.989
E	149.9989	1.69	91.0576	71.414

Orientierungen und Stationsabrisse

Stand­Pname	Ziel­Pname	t	r	o
A	P	300.00509	299.9993	0.0057929

Horizontaldistanzen und Höhendifferenzen

Punkt­namen		Hori­zontal­distan­zen e			Höhen­differen­zen dh
von	nach	Vor­blick	Rück­blick	Mittel­wert	Vor­blick	Rück­blick	Mittel­wert
A	1	70.706428		70.706428	9.9790681		9.979068
1	2		49.99889	49.998890		10.019655	10.019655
2	E	70.710514		70.710514	9.9987396		9.998740

Horizontalrichtungsabschlüsse

Kein Horizontalrichtungsabschluss berechenbar.

Koordinatenabschlüsse

	Verbesserungen				neue Koordinaten
Punktname	X	Y	Z	X	Y	Z
A	3.5239e-7	-0.004405	0.0093	99.996000352	99.999595415	100.00727
1				149.988988978	150.000595200	109.98634
2				149.985847165	199.999484630	120.00599
E	-3.524e-7	0.004405	-0.0093	99.983999648	249.997404585	130.00473

Die endgültig berechneten Koordinaten weichen von den wahren Koordinaten, die Grundlage der Simulation waren, um maximal 16 mm ab. Angesichts der simulierten Koordinaten- und Messabweichungen sind diese Abweichungen realistisch.

≡ START Anleitung English Lösung mit Universalrechner

IN DUBIO PRO GEO Tachymetrie : Universalrechner

Aus Punktkoordinaten und polaren Messwerten werden alle möglichen Größen berechnet. Rechenregeln zwischen diesen Größen werden aufgestellt und nacheinander angewendet, bis keine neuen Werte mehr erhalten werden, und zwar auf jede mögliche Weise. Dadurch ergeben sich oft viele verschiedene Ergebnisse, deren Vergleich zur Aufdeckung grober Fehler genutzt werden kann. Die Mediane der berechneten Werte stellen dann das Ergebnis einer robusten Schätzung dar.

Das Eingabe-Formular des Universalrechners ist praktisch identisch zum Formular der Polygonzugauswertung. Siehe oben.

Probieren Sie es aus: liefert in Auszügen Folgendes:

IN DUBIO PRO GEO Tachymetrie : Universalrechner

Das Protokoll des Universalrechners ist am Anfang identisch zum Protokoll der Polygonzugauswertung. Siehe oben.

Ergebnisse

Größe	von	nach	Werte	Minimum	Median	Maximum	IQR
X	E			99.97909864	99.98095414	99.98400000	4.7e-4
Y	E		1+5	249.99300000	249.99995340	250.09450093	0.0019
X	2			149.98189525	149.98381756	149.99566846	0.0030
Y	2		13	199.99305001	200.00304796	200.09759614	0.0058
X	1			149.98611812	149.98949599	150.08065237	0.0707
Y	1		4	150.00415902	150.00753757	150.09871225	0.0707
Z	A		1+7	99.99800000	100.01810738	100.01890852	0.0011
Z	E		1+7	129.99309148	129.99389262	130.01400000	0.0015
Z	1		9	109.97706807	109.99698332	109.99797668	0.0018
Z	2		9	119.99435186	119.99672260	120.01663784	0.0203
dh	1	2	17	9.99728370	9.99965453	10.01956977	0.0021
⁞				⁞	⁞	⁞	⁞
v	1	2	20	87.40821649	87.43330000	87.43381870	0.0242

Für die Lagekoordinaten X,Y von Punkt 1 wurden 4 Rechenwege gefunden, für die von Punkt 2 sind es 13 Rechenwege. Für die Höhenkoordinaten Z von Punkt 1 und Punkt 2 wurden je 9 Rechenwege gefunden. Die endgültig berechneten Koordinaten (Mediane) weichen von den wahren Koordinaten, die Grundlage der Simulation waren, um maximal 19 mm ab. Angesichts der simulierten Koordinaten- und Messabweichungen sind diese Abweichungen realistisch. Die IQRs der verschiedenen Lösungen liegen bei maximal 71 mm, was beweist, dass es keine unnormalen Widersprüche zwischen den Messwerten gibt.

Winkeleinheit = Gon. Die Erdkrümmung wurde korrigiert mit R=6371000.

≡ START Anleitung English Erweiterte Lösung

Als Nächstes soll versucht werden, noch mehr Rechenwege zu finden. Dazu muss man wissen, dass der Universalrechner Rechenregeln nur dort anwendet, wo Ziellinien verlaufen, also hier entlang des Polygonzugs. Z.B. zwischen A und 2 oder zwischen 1 und E verläuft keine Ziellinie, so dass im Dreieck A12 oder 12E nicht gerechnet wird. Will man das erreichen, fügt man einfach blinde Zielpunkte ein.

IN DUBIO PRO GEO Tachymetrie : Universalrechner

Aus Punktkoordinaten und polaren Messwerten werden alle möglichen Größen berechnet. Rechenregeln zwischen diesen Größen werden aufgestellt und nacheinander angewendet, bis keine neuen Werte mehr erhalten werden, und zwar auf jede mögliche Weise. Dadurch ergeben sich oft viele verschiedene Ergebnisse, deren Vergleich zur Aufdeckung grober Fehler genutzt werden kann. Die Mediane der berechneten Werte stellen dann das Ergebnis einer robusten Schätzung dar.

Winkeleinheit Gon [-200...200]    Notiz

Bekannte Punkte	Punktnamen und Koordinaten
Systemtyp: X Y Z linkshändig Spaltenformat: Punktname Koordinaten	P 100.004 0.002 // Höhe fehlt A 99.996 100.004 99.998 E 99.984 249.993 130.014 Die Reihenfolge der bekannten Punkte ist beliebig.

Punktnamen (Spalte 1) und Messwerte (Spalte 2…5)

zweite Spalte: Instrumentenhöhe dritte Spalte: Code / nicht benutzt vierte Spalte: Code / nicht benutzt fünfte Spalte: Code / nicht benutzt Format Zielpunktzeile zweite Spalte: Horizontalrichtung dritte Spalte: Zielhöhe vierte Spalte: Zenitwinkel fünfte Spalte: Schrägdistanz

A 1.69 P 299.9993 1 50.0006 1.71 91.0568 71.410 2 // blinder Zielpunkt E // blinder Zielpunkt ~~~~~~~~~~~~~ Trennzeile ~~~~~~~~~~~~~ 1 1.71 A 250.0017 1.68 2 100.0006 1.69 P // blinder Zielpunkt E // blinder Zielpunkt ~~~~~~~~~~~~~ Trennzeile ~~~~~~~~~~~~~ 2 1.69 1 300.0004 1.71 112.5667 50.989 E 149.9989 1.69 91.0576 71.414 P // blinder Zielpunkt A // blinder Zielpunkt Die Reihenfolge der Standpunkte und der Zielpunkte je Standpunkt ist beliebig.

Probieren Sie es aus: liefert in Auszügen Folgendes:

IN DUBIO PRO GEO Tachymetrie : Universalrechner

Unvollständig angeschloss. Polygonzug

3 benutzte bekannte Punkte: lokal, kartesisches Linkssystem

IN DUBIO PRO GEO erkennt automatisch, was zu rechnen ist.

Punktname	X	Y	Z
P	100.004	0.002
A	99.996	100.004	99.998
E	99.984	249.993	130.014

Eingabe-Messwerte

StandPname	ih
A	1.69

r = Horizontal- richtung
th = Zielhöhe
v = {Zenitwinkel}
s = Schrägdistanz

ZielPname	r	th	v	s
P	299.9993
1	50.0006	1.71	91.05680	71.41
2
E

StandPname	ih
1	1.71

Blinde Zielpunkte erhöhen die Anzahl der Rechen-
ergebnisse.

ZielPname	r	th	v	s
A	250.0017	1.68
2	100.0006	1.69
E
P

StandPname	ih
2	1.69

ZielPname	r	th	v	s
1	300.0004	1.71	112.5667	50.989
E	149.9989	1.69	91.0576	71.414
P
A

Ergebnisse

Größe	von	nach	Werte	Minimum	Median	Maximum	IQR
X	E			99.97909864	99.98095414	99.98400000	4.7e-4
Y	E		1+5	249.99300000	249.99995340	250.09450093	0.0019
X	1			149.98611812	149.99101850	149.99486141	0.0020
Y	1		11	149.99789004	150.00206370	150.00906039	0.0031
X	2			149.98196122	149.98754661	149.99381354	0.0057
Y	2		19	199.99305001	199.99987175	200.09759614	0.0052
Z	A		1+8	99.99800000	100.01829951	100.02066879	5.8e-4
Z	E		1+8	129.99133121	129.99370049	130.01400000	6.9e-4
Z	1		9	109.97706807	109.99698332	109.99797668	0.0018
Z	2		9	119.99435186	119.99672260	120.01663784	0.0203
dh	A	1	5	9.99493706	9.999677144	10.01997668	6.1e-4
⁞				⁞	⁞	⁞	⁞
v	1	2	17	87.40896212	87.43381870	87.43381883	0.0236

Für die Lagekoordinaten X,Y von Punkt 1 wurden 11 Rechenwege gefunden, für die von Punkt 2 sind es 19 Rechenwege. Für die Höhenkoordinaten Z von Punkt 1 und 2 wurden 9 Rechenwege gefunden. Die endgültig berechneten Koordinaten (Mediane) weichen unverändert von den wahren Koordinaten um maximal 19 mm. Die IQRs der verschiedenen Lösungen liegen jetzt nur noch bei maximal 20 mm, weil mehr Rechenwege gefunden wurden.

Winkeleinheit = Gon. Die Erdkrümmung wurde korrigiert mit R=6371000.

≡ START Anleitung English Lösung mit grobem Fehler in einem bekannten Punkt

Der Universalrechner kann mehr: Probieren Sie die Wirkung eines groben Fehlers in einem bekannten Punkt aus. Setzen Sie z.B. die X-Koordinate von P um 1 Meter herauf, auf 101.004. Die Ergebnisse der vorangegangenen Berechnung ändern sich wie folgt:

Ergebnisse

Größe	von	nach	Werte	Minimum	Median	Maximum	IQR
X	E			98.47924614	98.48112027	99.98400000	0.0473
Y	E		1+6	249.99044860	249.99300000	250.08777902	0.0482
X	1			149.48365272	149.99269686	150.97308942	0.0637
Y	1		18	149.90637407	150.00183245	152.02135606	0.0712
X	2			148.97954253	149.98924585	150.48429638	0.7045
Y	2		28	199.02461936	200.04435156	200.59336701	0.4974
Z	A		1+8	99.99800000	100.11772598	100.31156868	0.1475
Z	E		1+8	129.70043132	129.89427402	130.01400000	0.1486
Z	1		10	109.69119389	110.12158803	110.29943455	0.1836
Z	2		10	119.70169170	120.00599149	120.31580799	0.2468
dh	A	1	5	9.71319389	10.01760586	10.32143455	0.0185
⁞				⁞	⁞	⁞	⁞
v	2	E	1+4	90.90591539	91.03778239	91.05760000	0.0869

Die IQRs der über die verschiedenen Rechenwege erhaltenen Koordinatenwerte sind jetzt deutlich größer, bis zu 0.7 m, was anzeigt, dass ein Problem besteht. Die endgültig berechneten Koordinaten (Mediane) sind jedoch fast, teilweise sogar völlig, unverändert geblieben. Nur die Höhe von Punkt 1 weist eine Abweichung von 0.12 m auf. Die Tolerierung weniger grober Fehler bezeichnen wir als Robustheit.

≡ START Anleitung English