
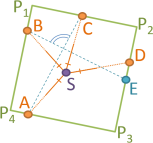
An den Wänden eines quadratischen Innenraumes wurden mit Tachymeter oder Laserscanner im Standpunkt S vier Zielpunkte A,B,C,D wie in der Abbildung dargestellt erfasst. Dabei wurden folgende Messwerte erhalten:
Zielpunkt Horizontalrichtung Horizontaldistanz A 0.000 gon 7.142 m B 115.549 gon 7.236 m C 181.534 gon 7.509 m D 249.345 gon 8.732 m
Berechnen Sie die Seitenlänge des Quadrats P1P2P3P4.
Richtungswinkel und Distanz AC
| PName | Y | X | |
|---|---|---|---|
| S | 100 | 100 |
t steht für Richtungswinkel und e für Horizontaldistanz.
Rechenablauf: Zunächst werden aus Richtungswinkeln und Distanzen die Koordinaten der Zielpunkte im Standpunktsystem erhalten. Letztlich werden daraus der Richtungswinkel AC 190.5341 gon und die zugehörige Seitenlänge mit 14.4973 m in diesem System erhalten.
IN DUBIO PRO GEO findet den Rechenweg allein.
| StandPname | ||||
|---|---|---|---|---|
| S |
| ZielPname | t | e |
|---|---|---|
| A | 0 | 7.142000 |
| B | 115.5490 | 7.236000 |
| C | 181.5340 | 7.509000 |
| D | 239.3450 | 8.732000 |
| StandPname | ||||
|---|---|---|---|---|
| A |
| ZielPname | t | e | |||
|---|---|---|---|---|---|
| C |
| StandPname | ||||
|---|---|---|---|---|
| A |
| ZielPname | t | e | |||
|---|---|---|---|---|---|
| C |
| Größe | von | nach | Werte | Minimum | Median | Maximum … |
|---|---|---|---|---|---|---|
| X | A | 107.1420000 | ||||
| Y | A | 1 | 100.0000000 | |||
| X | B | 98.25017616 | ||||
| Y | B | 1 | 107.0212401 | |||
| X | C | 92.80468256 | ||||
| Y | C | 1 | 102.1476704 | |||
| X | D | 93.76234428 | ||||
| Y | D | 1 | 93.88939649 | |||
| e | A | C | 1 | 14.49728110 | ||
| t | A | C | 1 | 190.5340838 |
Winkeleinheit = Gon.
Berechnung des Quadrats
Rechenablauf: Nachdem E berechnet ist, erhält man der Reihe nach über Rückwärtsschnitte P2, P1, P4 und zuletzt P3. Die Längen der drei berechneten Seiten stimmen überein mit 13.73 m. Die Richtungswinkel unterscheiden sich um exakt 100 gon. Damit haben wir ein Quadrat erhalten.
| Größe | von | nach | Werte | Min. | Median | Max … |
|---|---|---|---|---|---|---|
| X | E | 96.10313049 | ||||
| Y | E | 1 | 92.68386332 | |||
| X | P1 | 95.93009052 | ||||
| Y | P1 | 1 | 108.2163743 | |||
| X | P2 | 89.64394959 | ||||
| Y | P2 | 1 | 96.01036625 | |||
| X | P3 | 101.8499410 | ||||
| Y | P3 | 1 | 89.72423386 | |||
| X | P4 | 108.1360820 | ||||
| Y | P4 | 1 | 101.9302419 | |||
| ⁞ | ⁞ | |||||
| e | P1 | P2 | 1 | 13.72961033 | ||
| e | P1 | P4 | 1 | 13.72959168 | ||
| e | P3 | P4 | 1 | 13.72961033 | ||
| ⁞ | ⁞ | |||||
| t | P1 | P2 | 1 | 269.7237322 | ||
| t | P1 | P4 | 1 | 369.7237322 | ||
| t | P3 | P4 | 1 | 69.72373218 | ||
| ⁞ | ⁞ | |||||
Alle Ergebnisse sind korrekt.
Die Seitenlänge des Quadrats kontrolliert man am besten mit dem Umfang/4:
54.9184 m/4 = 13.7296 m
Das stimmt überein mit der Diagonale/√2:
19.4165 m/√2 = 13.7295 m
(Die Diagonale ist hier der ''Polygondurchmesser''.)
Auch das bestätigt die Richtigkeit des Ergebnisses.
| PName | Y | X | Polygonw. |
|---|---|---|---|
| P1 | 108.21637428 | 95.93009052 | 100 |
| C | 102.14770000 | 92.80470000 | 200 |
| P2 | 96.01036625 | 89.64394959 | 100 |
| D | 93.88940000 | 93.76230000 | 200 |
| P3 | 89.72423386 | 101.84994104 | 100 |
| A | 100.00000000 | 107.14200000 | 200 |
| P4 | 101.93024189 | 108.13608197 | 100 |
| B | 107.02120000 | 98.25080000 | 200 |
⁞
Flächeninhalt 188.50194379 Umfang 54.918404025
Polygondurchmesser19.416587949 zwischen P1 und P3
|
|
|
|