
Zur Zeit werden Koordinatenlisten von folgenden Rechenwerkzeugen benutzt:
|
|
|
|
| Außerdem kann man solche Listen erzeugen mit | ||
Leerzeilen und reine Kommentarzeilen werden ignoriert.
In allen anderen Zeile einer Koordinatenliste wird je ein Punkt definiert. Jede Zeile besteht aus drei bis fünf durch Tabulator, Leerzeichen oder Semikolon (= Spaltentrennzeichen) getrennten Feldern:
Die Reihenfolge der Zeilen in einer Koordinatenliste ist beliebig, außer bei Polygonberechnungen und beim Linienmaßstabsfaktor, wo die Reihenfolge das Polygon oder die Linie definiert.
Jede Koordinatenliste benötigt einen Koordinatensystemnamen, das ist eine fast beliebige Zeichenkette mit Einschränkungen wie bei Punktnamen, einen Koordinatensystemtyp und ein Spaltenformat.
Folgende Typen werden unterschieden:
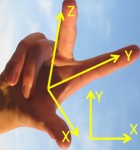
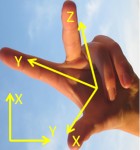
Folgendes ist zu beachten:
Folgende Formate werden unterschieden:
| Punktname Koordinaten | Punktname Code Koordinaten | Koordinaten |
|---|---|---|
| Beispiel: | Beispiel: | Beispiel: |
P1 23.06 16.10 17.11 Q2 14.02 19.63 17.05 007 63.3 44 //Lagepunkt | P1 Code1 23.06 16.10 17.11 Q2 Code1 14.02 19.63 17.05 007 Code2 63.3 44 //Lagepunkt //Code wird z.Z. ignoriert | 23.06 16.10 17.11 14.02 19.63 17.05 63.3 44 //Lagepunkt //Punkte werden //automatisch benannt |
Alle drei Listen sind identisch, nur bei der letzten werden die Punkte automatisch benannt. Standard für die automatische Benennung von Punkten ist 1,2,3,… Andere Optionen können über die festgelegt werden. Beachten Sie hierzu die folgenden Beispiele:
| Startname | Schrittweite | automatische Punktnamen |
|---|---|---|
| 1 (Standard) | 1 (Standard) | 1; 2; 3; … |
| 10 | 100 | 10; 110; 210; … |
| 10 | -100 | 10; -90; -190; … |
| abc10 | 100 | abc10; abc110; abc210; … |
| abc10 | -100 | abc10; abc-90; abc-190; … |
| abc | 100 | abc0; abc100; abc200; … |
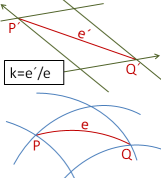
Gittersysteme (Systemtyp: Nordwert Ostwert Höhe oder Ostwert Nordwert Höhe) basieren auf einer lokalen Verebnung des gekrümmten Rotationsellipsoids mittels Gaußscher Abbildung (= Transversale Mercator-Abbildung auf dem Ellipsoid). Wegen der unvermeidbaren Verzerrungen stimmt die Gitterkoordinateneinheit nicht mit der metrischen Längeneinheit überein. Resultierend aus der Winkeltreue der Gaußschen Abbildung ist der Gittermaßstabsfaktor k für ein kleines Punktgebiet etwa konstant und wird automatisch berechnet.
Einzelheiten dazu finden Sie hier:
Bei Berechnungen mit Gitterkoordinaten wird vorausgesetzt, dass alle anderen metrischen Werte und Maßstäbe nicht mit dem Gittermaßstab behaftet sind.
Einzelheiten dazu finden Sie hier: Andere metrische Werte und Maßstäbe
Möchten Sie nicht für ein ganzes Punktgebiet, sondern für jeden einzelnen Punkt einen genauen Gittermaßstab berechnen, nutzen Sie das Rechenwerkzeug .

Die  stellt einen Referenzpunkt zur Überprüfung Ihres mobilen Navigationsgeräts zur Verfügung. Im
mit ellipsoidischer Höhe h
hat der Punkt folgende Koordinaten:
stellt einen Referenzpunkt zur Überprüfung Ihres mobilen Navigationsgeräts zur Verfügung. Im
mit ellipsoidischer Höhe h
hat der Punkt folgende Koordinaten:
| λ = 13.734806°, | φ = 51.033778°, | h = 160.5 |
| oder | ||
| λ = 13°44`.0884, | φ = 51°2`.0267, | h = 160.5 |
| oder | ||
| λ = 13°44`5``.304, | φ = 51°2`1``.602, | h = 160.5 |
| oder | ||
| E = 33U 411287.9 m, | N = 5654342.8 m, | h = 160.5 |
Wir geben nachfolgend verschiedene äquivalente Schreibweisen für die Koordinaten dieses Punktes. Alternative Schreibweisen für Länge und Breite erläutert Maßeinheiten . In dieser Tabelle ist das gewählte Ausgabedezimaltrennzeichen nicht wirksam.
| Einstellungen | Schreibweise der Koordinaten | Bemerkung |
|---|---|---|
| Systemtyp Länge Breite Höhe , Einheit der Länge/Breite Grad , Spaltenformat Punkt Koordinaten | HTW-Referenzpunkt 13.734806 51.033778 160.5 | |
| und nun mit Spaltenformat Punkt Code Koordinaten | HTW-Referenzpunkt Pfeiler 13.734806 51.033778 160.5 | |
| und nun mit Spaltentrennzeichen Semikolon | HTW-Referenzpunkt;Pfeiler; 13.734806;51.033778;160.5 | |
| und nun mit Spaltenformat Koordinaten | 13,734806 51,033778 160.5 | Eingabe wahlweise mit Dezimalkomma |
| und nun mit Einheit Länge/Breite GradMin | 13.440884 51.020267 160.5 | Format ggg.mmddddd |
| und nun mit Einheit Länge/Breite GradMinSek | 13.4405304 51.0201602 160.5 | Format ggg.mmssddd |
| und nun ohne Höhenangabe | 13.4405304 51.0201602 | nicht in allen Rechenwerkzeugen möglich |
| und nun mit alternativer Schreibweise für Winkel | 13.44`05.304`` 51°02`01.602`` | Maßeinheiten |
| und nun mit Systemtyp Breite Länge Höhe | 51.0201602 13.4405304 160.5 m | Was nach der dritten Koordinate auf der Zeile folgt, wird ignoriert (hier m) |
| und nun mit Systemtyp Ostwert Nordwert Höhe | 411287.9 5654342.8 160.5 m | |
| und nun mit Systemtyp Nordwert Ostwert Höhe | 5654342.8 411287,9 160,5 | Eingabe wahlweise mit Dezimalkomma |
| und nun mit dem Ostwert vorangestellter Zonennummer | 5654342.8 33411287.9 160.5 | Beim Ostwert werden nur 6 Ziffern vor dem Dezimaltrennzeichen ausgewertet. |
| und nun mit dem Ostwert vorangestellter letzter Ziffer der Zonennummer | 5654342.8 3411287.9 160.5 | |
| und nun mit gekürzten Koordinaten | 54342.8 11287.9 160.5 | Verwenden Sie falscher Nordwert=-5600000 und falscher Ostwert= 100000 |
| und nun ohne Höhenangabe | 54342.8 11287.9 | nicht in allen Rechenwerkzeugen möglich |
| und nun mit Systemtyp X Y Z rechtshändig | 3904281.170 954274.291 4936033.017 | |
| und nun mit Systemtyp Y X Z rechtshändig | 954274.291 3904281.170 4936033.017 | |
Koordinatenlisten können
Zwei gespeicherte Koordinatenlisten können gleichzeitig verwaltet werden. Beim Filtern und Sortieren nach Punktnamen erfolgt der Vergleich lexikographisch, das bedeutet, dass z.B. 1610 zwischen 10 und 20 liegt. Groß- und Kleinschreibung wird unterschieden. Der Vergleich von Koordinaten erfolgt selbstverständlich numerisch.
Die dritten Koordinaten (Z oder Höhe) einer Liste können wie folgt manipuliert werden:
Eine gefilterte und/oder sortierte Liste kann in einige Rechenwerkzeuge geladen und weiterverarbeitet werden oder auch in ''Liste bearbeiten/ansehen'' geladen werden, wobei die Original-Liste überschrieben wird.
Sollten in den Koordinatenlisten der berechneten Punkte für Sie nicht genügend Dezimalziffern angezeigt werden, wird empfohlen, diese Listen in einen neuen Browser-Tab oder in eine neue Liste zu laden. Sie sehen dann mehr Dezimalziffern.
Beim Speichern einer Liste werden eventuell zuvor schon gespeicherte Listen überschrieben. Aber zum Ansehen der Liste in oder oder in einem neuem Tab ist das nicht nötig.
Falls Sie überlange Punktnamen verwenden, werden diese in Tabellen abgeschnitten, meist auf 12, manchmal auch 9 führende Zeichen. Sie erhalten eine Warnung. Um die Punktnamen in voller Länge zu sehen, kann derselbe Trick angewendet werden.
Siehe Koordinatenlisten filtern, speichern und laden.
|
|
|
|