
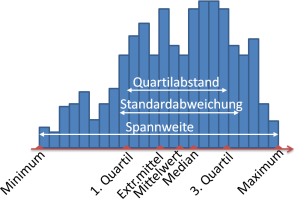
Der Quartilabstand (auch Interquartilabstand) ist der Abstand des ersten und dritten Quartils (Viertelwerts). Innerhalb dieses Intervalls liegen 50% aller Werte einer Größe. Für die Berechnung des Quartilabstands werden mindestens 12 Messwerte benötigt.
Die Schiefe
zeigt an, wie symmetrisch oder unsymmetrisch die Messwert-Verteilung ist.
Die Exzess-Kurtosis
zeigt an, wie flach- oder steilgipflig die Messwert-Verteilung ist, im Vergleich zur Normalverteilung.
| Schiefe | Verteilung | Exzess-Kurtosis | Verteilung | |
|---|---|---|---|---|
| < 0 | linksschief | < 0 | flachgipflig | |
| = 0 | symmetrisch | = 0 | normale Form (Gauß-Glocke) | |
| > 0 | rechtsschief | > 0 | steilgipflig |
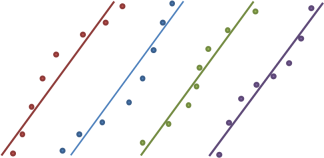
Dieser Plot stellt eine schnelle graphische Methode dar, um bei den Wiederholungsmessungen Abweichungen von der Normalverteilung festzustellen. Auf der horizontalen Achse sind die Messwerte aufgetragen und auf der vertikalen Achse die Mediane der zugehörigen normalen Ordnungsstatistiken. Im Fall einer Normalverteilung müssten alle Punkte im Plot etwa kollinear sein. Abweichungen davon können auf unsymmetrische (schiefe) oder steilgipflige, d.h. endlastige, oder flachgipflige Verteilungen hindeuten. Isoliert liegende Punkte links unten oder rechts oben in der Graphik sind ausreißerverdächtig.
Die Messwerte werden als unabhängige Realisierungen einer normalverteilten Zufallsvariable betrachtet. Wenn die Messwerte nur näherungsweise einer Normalverteilung folgen, liefern einige Tests immer noch korrekte Ergebnisse, wenn die Zahl der Messwerte nicht zu gering ist. Korrelationen würden das Ergebnis verfälschen.
Alle Tests werden berechnet, die theoretisch berechenbar sind, selbst wenn ein anderer Test mit geringerer Wahrscheinlichkeit eine falsche Entscheidung herbeiführen würde. Beispiel: Ist die Standardabweichung der Messwerte a priori korrekt bekannt, führt der w-Test nach Baarda seltener eine falsche Entscheidung als der Pope-Test und der Gauß-Test seltener eine falsche Entscheidung als der t-Test herbei.
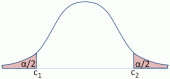
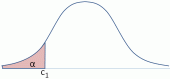
Annahmebereich : Die Nullhypothese Ho wird angenommen, wenn die Teststatistik
| N(μ,σ) | Normalverteilung mit Erwartungswert μ und Standardabweichung σ |
| t(r) | t-Verteilung mit r Freiheitsgraden |
| τ(r) | τ-Verteilung mit r Freiheitsgraden |
| χ²(r) | χ²-Verteilung mit r Freiheitsgraden |
| F(r,r') | F-Verteilung mit r und r' Freiheitsgraden |
Dieser Test überprüft für die Messwerte die Hypothese der Normalverteilung. Die Teststatistik bewertet die Differenz zwischen der empirischen Verteilung der Stichprobe und der Normalverteilung und gibt dabei mehr Gewicht auf die Enden der Verteilung, als klassische Tests wie z.B. der Cramér–von-Mises Test.
Der Anderson-Darling-Test wird in bis zu vier Varianten berechnet:
Die ersten drei Varianten setzen voraus, dass die erforderlichen Werte gegeben wurden.
Jährlich im dritten Semester werden im Studiengang Vermessung/ Geoinformatik der  von jedem Studierenden tachymetrische Bestimmungen derselben Punkte vorgenommen.
Diese können als unabhängige Wiederholungsmessungen angesehen werden.
In den Jahren 2010 und 2011 wurden für einen ausgewählten Punkt folgende Ergebnisse erhalten:
von jedem Studierenden tachymetrische Bestimmungen derselben Punkte vorgenommen.
Diese können als unabhängige Wiederholungsmessungen angesehen werden.
In den Jahren 2010 und 2011 wurden für einen ausgewählten Punkt folgende Ergebnisse erhalten:
| Jahr | Bestimmungen der Punkthöhe, Einheit=Meter |
|---|---|
| 2010 | 116.774 116.755 116.755 116.751 116.742 116.745 116.760 116.754 116.753 116.739 116.752 116.747 116.732 116.752 116.736 116.764 116.738 116.765 116.757 116.750 116.741 116.759 116.751 116.753 116.734 116.737 116.757 116.730 116.755 |
| 2011 | 116.764 116.748 116.758 116.743 116.757 116.659 116.744 116.754 116.761 116.762 116.769 116.741 116.747 116.738 116.744 116.750 116.746 116.736 116.760 116.762 116.760 116.756 116.739 116.754 116.728 116.745 116.737 116.750 |
Der Punkt hat im Übungnetz die bekannte Soll-Höhe 116.767 m . Von den Studierenden kann trotz fehlender Routine eine Bestimmung der Punkthöhe mit einer Standardabweichung von σo=0.01 m erwartet werden. Die Wiederholungsmessungen sollen mit einer Wahrscheinlichkeit für Entscheidungsfehler erster Art von α=0.05 statistisch getestet werden.
Der Normalverteilungsplot
zeigt die Verteilung der Messwerte (Punkte) relativ zu einer am besten passenden Normalverteilung (Gerade) an.
Sofort fällt auf, dass links unten ein roter (=2011) Punkt insoliert liegt. Dieser zeigt eindeutig einen Ausreißer an.
Die restlichen Punkte streuen etwa um die blaue (=2010) Gerade.
Im mittleren Bereich der Punkte (rund um den Median) liegen die blauen (=2010) Punkte etwas weiter rechts, als die roten (=2011).
Der Median der 2010er Messwerte ist also größer, nämlich um 3 mm.
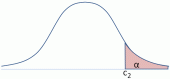
Zunächst kann man untersuchen, ob die geforderte Messgenauigkeit erreicht wurde, ob also Ho:σ≤σo anzunehmen ist. Das überprüft der rechtsseitige Globaltest, der bei der Messreihe Jahr 2011 abgelehnt wird. Also wurde die Messgenauigkeit hier wahrscheinlich nicht erreicht. Genauer gesagt, die Wahrscheinlichkeit, dass die Messgenauigkeit erreicht und der Globaltest trotzdem abgelehnt wurde, beträgt α=0.05.
Auch der w-Test nach Baarda zeigt für Jahr 2011 einen Ausreißer an. Dies ist der Messwert 116.659, der am weitesten vom Mittelwert entfernt liegt. Eliminiert man diesen Wert und wiederholt die Auswertung, wird sowohl der linksseitige Globaltest, als auch der w-Test angenommen. Allerdings könnte irritieren, dass auch der rechtsseitige Globaltest Ho:σ≥σo angenommen wird. Die Ursache für dieses Phänomen ist folgende: Wenn α klein genug gewählt wird, werden die Nullhypothesen für alle statistischen Tests stets angenommen. Und für nur wenige Messwerte ist α=0.05 praktisch schon sehr klein.
Wäre σo=0.01 nicht bekannt gewesen, hätte man den Ausreißer hier auch mittels τ-Test nach Pope aufdecken können.
Die Standardabweichungen einer einzelnen Bestimmung der Punkthöhe werden jetzt a posteriori mit 0.0107 m für Jahr 2010 und 0.0102 m für Jahr 2011 ermittelt. Die Antwort auf die Frage, ob nach Eliminierung des Ausreißers die Messgenauigkeiten beider Jahre als gleich zu bewerten sind, liefert der zweiseitige F-Test mit Ho:σx=σy. Diese Hypothese wird angenommen, also war die Genauigkeit im Jahr 2011 nicht signifikant höher.
Die Mittelwerte betragen 116.7496 m für Jahr 2010 und 116.7501 m für Jahr 2011. Die Antwort auf die Frage, ob nach Eliminierung des Ausreißers die Erwartungswerte beider Messreihen als gleich zu bewerten sind, liefert der Zweistichproben-Gauß-Test mit Ho:μx=μy . Diese Hypothese wird angenommen, also sind die Erwartungswerte als gleich zu betrachten.
Die Hypothese, dass der als Sollhöhe des Punktes bisher verwendete Wert μo=116.767 mit den Mittelwerten identisch ist, ist Gegenstand des zweiseitigen Einstichproben-Gauß-Tests mit Ho:μ=μo . Diese Hypothese wird für beide Jahre abgelehnt. Die Schlussfolgerung könnte lauten, dass die Sollhöhe nicht korrekt ist, oder dass in beiden Jahren dieselben systematischen Messabweichungen auftraten. In diesem Fall ist nur denkbar, dass eine in allen Bestimmungen gemeinsam verwendete Anschlusshöhe falsch war und dies bei der Stationshöhenbestimmung nicht auffiel.
Da beide Messreihen keine signifikanten Unterschiede aufweisen, kann man diese zu einer Messreihe vereinen und die Auswertung wiederholen:
Genau wie in allen bisherigen Fällen wird die Sollhöhe μo=116.767 zurückgewiesen. Dieser Wert ist entweder nicht korrekt oder die Höhen wurden systematisch falsch erhalten. Außerdem wird die Hypothese der Normalverteilung mit dem Parameter μo=116.767 abgelehnt. Ohne diesen Parameter ist der Anderson-Darling-Test erfolgreich.
Zwei Reihen normalverteilter Pseudozufallszahlen N(53.06;16.10) aus www.random.org/gaussian-distributions werden untersucht.
Eine Reihe Laplace-verteilter und eine Reihe χ²(1)-verteilter Pseudozufallszahlen, je 100 Werte, berechnet mit GNU Octave werden untersucht. Die wahren Parameter dieser Verteilungen sind
| Reihe | Erwartungswert | Median | Standardabweichung | Quartilabstand | Schiefe | Exzess-Kurtosis |
|---|---|---|---|---|---|---|
| Laplace | 0 | 0 | 1.414 | 1.386 | 0 | 3 |
| χ²(1) | 1 | 0.455 | 1.414 | 1.222 | 2.828 | 12 |
|
|
Ausgleichungslehrbücher |
|