
Die (linearisierten) Verbesserungsgleichungen l + v = A x werden nach der Methode der kleinsten Quadrate: vTP v = min!gelöst, bekannt auch als vermittelnde Ausgleichung (Gauß-Markov-Modell):
Optional können m (linearisierte) Bedingungsgleichungen BTx=b angegeben werden, die die wahren Parameter x erfüllen:
Ein Ausgleichungsproblem liegt nur vor, wenn n + m > u gilt. Im Moment werden nur
unterstützt. Überstrichene Größen symbolisieren Schätzwerte, also entweder ausgeglichene Größen x, l oder a posteriori Standardabweichungen σ.
Mindestens der Vektor der Beobachtungen l und die Designmatrix A müssen gegeben werden. Ihre Zeilenzahl muss gleich sein. Optional können die Beobachtungen und die Parameter mit Namen versehen werden. Diese erscheinen dann in den Ergebnistabellen.
Für jede Beobachtung können Sie einen Wert für die a priori Standardabweichung σ oder ein Gewicht p angeben. Im ersten Fall berechnet IN DUBIO PRO GEO die Gewichte für die Ausgleichung aus 1/σ². Standardabweichungen haben dieselbe Einheit wie die Beobachtungen und dürfen nicht negativ sein. Gewichte müssen positiv sein. Wird nur ein Wert gegeben, gilt dieser für alle Beobachtungen gleichermaßen. Wird kein Wert gegeben, werden alle Gewichte gleich Eins gesetzt.
Als Hauptergebnisse der Ausgleichung erhält man
Optional kann eine Bedingungsmatrix B und ein Bedingungsvektor b gegeben werden. Die Zeilen- und Spaltenzahl von B muss zu den Dimensionen von b und x passen. Alternativ kann auch die transponierte Matrix BT gegeben werden.
Die ausgeglichenen Parameter x werden in diesem Fall so berechnet, dass diese ebenso die linearen Bedingungsgleichungen erfüllen:
BT x = b
Oft ist man nicht direkt an den ausgeglichenen Größen x oder l selbst interessiert, sondern diese sind nur Hilfsgrößen auf dem Weg zu eigentlich gesuchten Größen f. Also berechnet man diese Größen als Funktionen ausgeglichener Größen. Ist diese Funktion linear in der Form f = F x oder f = F l, so gibt man direkt die Matrix F an und erhält f als Rechenergebnis. Für f werden a posteriori Standardabweichungen σf und auch a priori Standardabweichungen σf berechnet, das letzte aber nur, falls solche für die Beobachtungen gegeben waren.
Optional können die Funktionen mit Namen versehen werden. Diese erscheinen dann in den Ergebnistabelle.
Tritt noch ein Absolutglied fo hinzu, so dass f = fo + F x oder f = fo + F l, ändern sich die Standardabweichungen nicht. fo kann manuell addiert werden.
Statistische Tests werden nur berechnet, wenn eine Wahrscheinlichkeit für Entscheidungsfehler erster Art α gegeben wurde. Je kleiner dieser Wert ist, desto seltener wird bei den Tests die Nullhypothese abgelehnt.
Der Globaltest überprüft, ob a priori und a posteriori Standardabweichungen ausreichend gut übereinstimmen. Er ist damit nur anwendbar, wenn beide Werte berechnet werden konnten. Dieser Test deckt eine Reihe von möglichen Modellfehlern auf.
Zur Lokalisierung möglicher Ausreißer kann der τ-Test nach Pope oder der w-Test nach Baarda genutzt werden, der letzte aber nur, wenn a priori Standardabweichungen für die Beobachtungen gegeben wurden. In diesem Fall ist er vorzuziehen. Die Teststatistik für einen Ausreißer ist entweder max|SV| oder max|NV|. Falls diese den zugehörigen kritischen Wert überschreitet, ist ein Ausreißer aufgedeckt und lokalisiert in der Beobachtung, bei der das Maximum auftrat.
Außerdem werden (AIC, AICc, BIC) für das Ausgleichungsmodell berechnet.
Bei nichtlinearen Ausgleichungsmodellen L+v=φ(X) mit nichtlinearen Funktionen φ ist eine Linearisierung nötig, bei der ausgehend von einem Vektor der Näherungsparameter X0 gesetzt wird
x := X − X0, l := L-φ(X0)
und die Matrix A besteht aus allen partiellen Ableitungen ∂φ/∂X berechnet an der Stelle X=X0.
Eine solche Matrix heißt in der Mathematik Jacobi-Matrix.
Am Ende werden die ausgeglichenen Größen berechnet als
X = X0 + x, L = L + v
Die Schlussprobe L = φ(X) sollte erfüllt sein, sonst waren die Näherungsparameter zu schlecht und die Ausgleichung muss mit X0 := X wiederholt werden. Das Linearisieren muss manuell erledigt werden. Die Standardabweichungen für ungekürzte und gekürzte Parameter X, x und für ungekürzte und gekürzte Beobachtungen L, l sind identisch.
Sind nichtlineare Bedingungsgleichungen β(X) = 0 vorhanden, müssen auch diese linearisiert werden:
β(X0+x) = β(X0) + BTx = 0, b = -β(X0)
und die Matrix BT besteht aus den partiellen Ableitungen ∂β/∂X berechnet an der Stelle X = X0.
Bei nichtlinearen Funktionen f = ψ(X) müssen auch diese linearisiert werden:
ψ(X0 + x) = ψ(X0) + Fx = 0, fo = ψ(X0)
und die Matrix F besteht aus den partiellen Ableitungen ∂ψ/∂X berechnet an der Stelle X = X0. Die Standardabweichungen können wie zuvor direkt der Berechnung entnommen werden. Die Funktionswerte müssen manuell berechnet werden als ψ(X) oder ψ(Xo) + f . Diese Werte müssten bis auf Linearisierungsfehler gleich sein (Schlussprobe). Dieselbe Prozedur gilt für f = ψ(L).
Für nähere Erläuterungen zur Geodätischen Ausgleichung konsultieren Sie bitte die Ausgleichungslehrbücher.
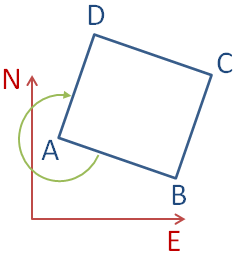
Die Ecken eines ebenen Quadrats wurden gemessen (E=Ost, N=Nord):
E [m] N [m]
A 17.11 14.02
B 39.37 8.26
C 45.13 30.53
D 22.80 36.30
Wegen geringer Messabweichungen beschreiben diese Punkte nicht exakt ein Quadrat. Dieses soll bestmöglich im Sinne kleinster Verbesserungsquadrate vTPv = min! für die Beobachtungen bestimmt werden. Außerdem suchen wir die Seitenlänge a und den Flächeninhalt F des ausgeglichenen Quadrats mit Genauigkeitsschätzungen.
Beobachtungen L sind die n = 8 gemessenen Koordinaten in der gewählten Reihenfolge EA,NA,EB,...,ND . Alle Beobachtungsstandardabweichungen σl können a priori mit 0.01 m angenommen werden. Korrelationen zwischen den Beobachtungen müssen, da unbekannt, vernachlässigt werden.
Tipp: Überzeugen Sie sich mit der Berechnung von ABCD in , dass ABCD näherungsweise quadratisch ist:
Ein Quadrat wird durch u = 4 Parameter eindeutig bestimmt. Wir wählen die Koordinaten der Punkte A und B als Parameter aus. Zur Unterscheidung von den Beobachtungen symbolisieren wir diese mit kleinen Buchstaben eA,nA,eB,nB und wählen diese Reihenfolge. Um die durch die Parameter beschriebenen Punkte A und B zu einem exakten Quadrat zu ergänzen, drehen wir den Vektor AB um 300 gon = 270° (⇑ Abbildung) und tragen diesen gedrehten Vektor an B und an A an. (Einen ebenen Vektor dreht man um 300 gon = 270°, indem man die beiden Komponenten vertauscht und bei der neuen Ost-Komponente das Vorzeichen ändert.) Das Quadrat mit den Parametern eA,nA,eB,nB hat also folgende weiteren Eckpunktkoordinaten:
| eC = eB - (nB - nA) | nC = nB + (eB - eA) | eD = eA - (nB - nA) | nD = nA + (eB - eA) |
Somit ergibt sich folgendes funktionale Ausgleichungsmodell L + v = φ(X):
| EA + vEA = eA | EB + vEB = eB | EC + vEC = eB - (nB - nA) | ED + vED = eA - (nB - nA) |
| NA + vNA = nA | NB + vNB = nB | NC + vNC = nB + (eB - eA) | ND + vND = nA + (eB - eA) |
Weil φ hier eine lineare Funktion ist, wäre von daher keine Linearisierung nötig, und wir könnten das soeben erstellte System der Verbesserungsgleichungen sofort mit l + v = A x identifizieren. Allerdings ist die Seitenlänge a eine nichtlineare Funktion der Parameter, und zur Berechnung der Genauigkeit von a ist eine Linearisierung letztlich doch nötig. Wir verwenden die gemessenen Koordinaten der Punkte A und B als Näherungsparameter X0 . Die gekürzten Beobachtungen l = L - φ(X0) lauten daher:
E [m] N [m]
A 17.11- 17.11 = 0.00 14.02- 14.02 =0.00
B 39.37- 39.37 = 0.00 8.26- 8.26 =0.00
C 45.13-(39.37-8.26+14.02)= 0.00 30.53-( 8.26+39.37-17.11)=0.01
D 22.80-(17.11-8.26+14.02)=-0.07 36.30-(14.02+39.37-17.11)=0.02
Die Designmatrix A und der Vektor der gekürzten Beobachtungen l lauten somit:
| A= |
| l= |
|
Zwei Funktionen von ausgeglichenen Parametern
a=[(eA-eB)²+(nA-nB)²]½, F= (eA-eB)²+(nA-nB)²
sind zu berechnen. Aus diesen Funktionen (in dieser Reihenfolge) gewinnen wir folgende Ableitungen, die in der Funktionalmatrix
| F= |
| = |
|
zusammengefasst werden. Zusammen mit den n = 8 a priori Standardabweichungen der Beobachtungen, die alle 0.01 betragen, sind die Eingangsgrößen komplett. Als Wahrscheinlichkeit für Entscheidungsfehler erster Art wählen wir 0.01.
Zunächst stellen wir fest, dass der Globaltest abgelehnt wird. Das bedeutet, dass die Genauigkeiten a priori und a posteriori signifikant verschieden sind. Alle ausgeglichenen Koordinaten haben dieselbe Standardabweichung von σl = 7.1 mm bzw. σl = 16.8 mm . (Die Genauigkeiten von gekürzten und ungekürzten Größen stimmen stets überein). Alle Redundanzanteile betragen r = 0.5 = 50% , was beweist, dass alle Beobachtungen gut kontrollierbar sind. Eine normierte Verbesserung NV = 4.6 führt zur Ablehnung der Nullhypothese des w-Tests. Die Beobachtung ED könnte hiernach grob falsch sein und die Ausgleichung könnte ohne diese Beobachtung wiederholt werden. Alle Studentisierten Verbesserungen SV liegen unterhalb ihres kritischen Wertes. Es ist auch möglich, dass die a priori Genauigkeitsannahme wohl doch etwas zu optimistisch war.
Mit den Verbesserungen v = A x - l berechnen wir die ausgeglichenen Beobachtungen L = L + v und damit die endgültigen Koordinaten der Eckpunkte:
E [m] N [m] A 17.11-0.0225=17.0875 14.02-0.0125=14.0075 B 39.37+0.0025=39.3725 8.26+0.0025= 8.2625 C 45.13-0.0125=45.1175 30.53+0.0175=30.5475 D 22.80+0.0375=22.8325 36.30-0.0075=36.2925
Wir überzeugen uns mit der Berechnung von ABCD mit endgültigen Koordinaten in , dass ABCD exakt ein Quadrat ist. Dies ist zugleich die Schlussprobe.
Die ausgeglichene Seitenlänge und den ausgeglichenen Flächeninhalt des Quadrats gewinnen wir aus endgültigen Koordinaten direkt aus der Schlussprobe von oben zu a = 23.01361 und F = 529.626. Dasselbe Ergebnisse erhalten wir auch mit den Abmessungen des Näherungsquadrats, welches sich aus den Näherungsparametern ergibt,
F0=(17.11-39.37)²+(14.02-8.26)²=528.685, a0 = √528.685=22.9932
plus gekürzter Funktionswerte f = F x , für die man der Ausgleichung die Werte 0.0204 und 0.940 entnimmt.
Die Genauigkeiten von a stimmen mit denen der ausgeglichenen Koordinaten überein, weil die Kofaktoren gleich sind. Die a posteriori Standardabweichung von F beträgt σF = 0.77 m².
Eliminieren Sie die Beobachtung ED durch Streichen der 7. Zeile der A-Matrix und Streichen der 7. gekürzten Beobachtung und der 7. Beobachtungsstandardabweichung. Wiederholen Sie nun die Ausgleichung. Es stellt sich heraus, dass jetzt alle Nullhypothesen angenommen werden. Alle a posteriori Standardabweichungen sind deutlich kleiner, für den ausgeglichenen Flächeninhalt z.B. 0.23 m². Dieses Vorgehen ist jedoch fraglich, weil es möglicherweise konsequenter wäre, den Punkt D insgesamt zu streichen. (Warum sollte nur eine Koordinate von D grob falsch sein?). Den statistischen Test, der diese Alternativhypothese entscheiden könnte, müsste man allerdings manuell erledigen.
und können mit neu ausgeglichen werden. Das bietet folgende Vorteile:
Demnächst werden noch mehr Werkzeuge diese Option bieten.
|
|
Ausgleichungslehrbücher |
|