The (linearised) residual equations l + v = A x are solved in the least squares sense: vTP v = min!also known as adjustment with observation equations (Gauss-Markov model):
Optionally you may specify m (linearised) constraints BTx=b , which are fulfilled by the true parameters x :
An adjustment problem only arises if n + m > u holds. At the moment only
are supported. Overlined quantities symbolise estimates, i.e. either adjusted quantities x, l or posterior standard deviations σ.
At least the vector of observations l and the design matrix A must be given. Their number of rows must be equal. Optionally, names can be assigned to the observations and to the parameters. They will appear in the result tables.
For all observations an a priori standard deviation σ or a weight p can be specified. In the first case IN DUBIO PRO GEO computes weights for the adjustment by 1/σ². Standard deviations have the same unit as the observations and must not be negative. Weights must be positive. If only one value is given, it is assigned to all observations. If no value is given, unit weights are assigned to all observations.
As main results of the adjustment, you obtain
Optionally, a constraints matrix B and a constraints vector b can be given. The number of rows and columns of B must match the dimensions of b and x . Alternatively, the transposed matrix BT can be given.
In this case the adjusted parameters x are computed such that they also fulfill these linear constraints:
BT x = b
Oftentimes, you are not directly interested in the adjusted quantities x or l , but they are mere auxiliary quantities on the way to the quantities f actually desired. Therefore, you compute these quantities as functions of adjusted quantities. If these functions are linear in the form f = F x or f = F l, then you directly specify the matrix F and obtains f as a result of the computations. For f a posteriori standard deviations σf and also priori standard deviations σf are computed, but the latter only, if those have been given for the observations.
Optionally, names can be assigned to the functions. They will appear in the result table.
If an absolute term fo is added, such that f = fo + F x or f = fo + F l, then the standard deviations do not change. fo may be added manually.
Statistical tests are only computed, if a probability of type I decision error α has been given. The smaller this value, the more rarely the null hypothesis is rejected in the tests.
The global test checks if a priori and a posteriori standard deviations are in good agreement. It is therefore only applicable, if both values could be computed. This test detects some possible model misspecifications.
For the localisation of outliers the τ test of Pope or the w test of Baarda can be used, but the latter only if a priori standard deviations have been given for all observations. In this case it is preferable. The test statistic for one outlier is either max|SV| or max|NV|. If this exceeds the corresponding critical value, an outlier is detected and localised in the observation, where the maximum is assumed.
Moreover, (AIC, AICc, BIC) are computed for the adjustment model.
For nonlinear adjustment models L+v=φ(X) with non-linear functions φ a linearisation is required, where starting from an approximate parameter vector X0 we set
x := X − X0, l := L-φ(X0)
and the matrix A
consists of all partial derivatives
∂φ/∂X computed at the location X=X0.
In mathematics such a matrix is called Jacobian matrix.
Finally, the adjusted quantities are computed as
X = X0 + x, L = L + v
The final control condition L = φ(X) should be satisfied, otherwise the approximate parameters were too bad and the adjustment has to be repeated with X0 := X . The linearisation has to be carried out manually . The standard deviations of original and linearised parameters X, x and of original and linearised observations L, l are identical.
If nonlinear constraints β(X) = 0 are given, they must be linearised too:
β(X0+x) = β(X0) + BTx = 0, b = -β(X0)
and the matrix BT consists of partial derivatives ∂β/∂X computed at the location X = X0.
If nonlinear functions f = ψ(X) are given, they must be linearised too:
ψ(X0 + x) = ψ(X0) + Fx = 0, fo = ψ(X0)
and the matrix F consists of partial derivatives ∂ψ/∂X computed at the location X = X0. As before, the standard deviations can be obtained directly from the computation. The functional values must be computed manually by ψ(X) or ψ(Xo) + f . These values must be identical apart from linearisation errors (final control condition). The same procedure applies to functions f = ψ(L).
For more details on geodetic adjustment please seek advice from the Adjustment textbooks.
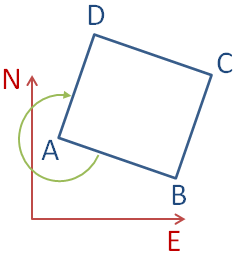
The vertices of a planar square have been measured (E=East, N=North):
E [m] N [m]
A 17.11 14.02
B 39.37 8.26
C 45.13 30.53
D 22.80 36.30
Due to small measurement errors these points do not exactly form a square. These errors must be adjusted in the sense of least squares of residuals vTPv = min! for the observations. Moreover, the length of a side a and the area F of the adjusted square with accuracy estimates are required.
Observations L are the n = 8 measured coordinates in the chosen succession EA,NA,EB,...,ND All observation standard deviations σl are a priori assumed as 0.01 m . Correlations between these observations must be neglected because they are unknown.
Tip: See for yourself by the computation of ABCD in , that ABCD is approximately square:
A square is determined uniquely by u = 4 parameters . We choose the coordinates of the points A and B as parameters. To discriminate between observations and parameter, the latter are symbolised by small letters eA,nA,eB,nB and this succession is chosen. To complete the points A and B described by these parameters to an exact square we rotate the vector AB by 300 gon = 270° (⇑ figure) and stake out points C and D from B and A by this vector. (A planar vector is rotated by 300 gon = 270° by interchanging both components and changing the sign of the new east component.) Hence, the square with the parameters eA,nA,eB,nB has the following additional vertex coordinates:
| eC = eB - (nB - nA) | nC = nB + (eB - eA) | eD = eA - (nB - nA) | nD = nA + (eB - eA) |
Therefore, we come up the following functional adjustment model L + v = φ(X):
| EA + vEA = eA | EB + vEB = eB | EC + vEC = eB - (nB - nA) | ED + vED = eA - (nB - nA) |
| NA + vNA = nA | NB + vNB = nB | NC + vNC = nB + (eB - eA) | ND + vND = nA + (eB - eA) |
Since φ is a linear function, no linearisation is immediately required and we could identify the derived system of observation equations with l + v = A x . However, the side length a is a non-linear function of the parameters, and for the computation of the accuracy of a a linearisation is finally required nonetheless. We use the observed coordinates of points A and B as approximate parameters X0 . The linearised observations l = L - φ(X0) read therefore:
E [m] N [m]
A 17.11- 17.11 = 0.00 14.02- 14.02 =0.00
B 39.37- 39.37 = 0.00 8.26- 8.26 =0.00
C 45.13-(39.37-8.26+14.02)= 0.00 30.53-( 8.26+39.37-17.11)=0.01
D 22.80-(17.11-8.26+14.02)=-0.07 36.30-(14.02+39.37-17.11)=0.02
Hence, the design matrix A and the vector of linearised observations l read:
| A= |
| l= |
|
Two functions of adjusted parameters
a=[(eA-eB)²+(nA-nB)²]½, F= (eA-eB)²+(nA-nB)²
need to be computed. From these functions (in this succession) we derive the following derivatives, which constitute the Jacobian matrix
| F= |
| = |
|
Together with the n = 8 prior standard deviations of the observations, which all amount to 0.01 , the input quantities are complete. As a probability of type I decision error we choose 0.01.
First of all, we realise that the global test (overall model test) is rejected. This means that the prior and posterior accuracies are significantly different. All adjusted coordinates have the same standard deviation of σl = 7.1 mm or rather σl = 16.8 mm . (The accuracies of original and linearised quantities are always the same.) All redundancy parts amount to r = 0.5 = 50% , which proves that all observations are well controllable. A normalised residual NV = 4.6 causes a rejection of the null hypothesis of the w test. The observation ED could accordingly be grossly erroneous and the adjustment could be repeated without this observation. All studentised residuals SV are below their critical value. Therefore, it is also possible that the prior accuracy assumption was overly optimistic.
By means of the residuals v = A x - l we compute the adjusted observations L = L + v and thereby the final coordinates of the vertices:
E [m] N [m] A 17.11-0.0225=17.0875 14.02-0.0125=14.0075 B 39.37+0.0025=39.3725 8.26+0.0025= 8.2625 C 45.13-0.0125=45.1175 30.53+0.0175=30.5475 D 22.80+0.0375=22.8325 36.30-0.0075=36.2925
We confirm by the computation of ABCD with final coordinates in , that ABCD is exactly square. This is immediately the final control condition.
The adjusted side length and the adjusted area of the square we find directly from the final control computation above a = 23.01361 und F = 529.626. The same result we obtain by the size of the approximate square, which is defined by the approximate parameters,
F0=(17.11-39.37)²+(14.02-8.26)²=528.685, a0 = √528.685=22.9932
plus linearised function values f = F x , for which the adjustment gives the values 0.0204 und 0.940 .
The accuracies of a coincide with those of the adjusted coordinates because the cofactors are the same. The posterior standard deviation of F assumes the value σF = 0.77 m².
Eliminate the observation ED by erasing the 7th row of the matrix A , erasing the 7th linearised observation and the 7th observation standard deviation. Now repeat the adjustment. It turns out that all null hypotheses are now accepted. All posterior standard deviations assume considerably smaller values, e.g. for the adjusted area 0.23 m². However, this approach is disputable because is would be more consequential to fully erase the point D. (Why should only one coordinate of D be grossly erroneous?). But the statistical test for the decision of this alternative hypothesis you have to do manually.
and can be re-adjusted with . This yields the following advantages:
Forthcoming: More tools will provide this option.
|
|
Ausgleichungslehrbücher |
|
| Link | Author(s) | Title | Year | Type | Pages MByte |
|---|---|---|---|---|---|
 | Halsig S, Ernst A, Schuh WD | Ausgleichung von Höhennetzen aus mehreren Epochen unter Berücksichtigung von Bodenbewegungen | 2013 | 9 0.1 | |
|
| Bezirksregierung Köln | Ausgleichung im Liegenschaftskataster | 2009 | 98 0.1 | |
|
| Boysen A | Beurteilung von Softwarepaketen zur Ausgleichungsrechnung | 2009 | 120 0.1 | |
|
| Neitzel F, Petrovic S | Total Least Squares (TLS) im Kontext der Ausgleichung nach kleinsten Quadraten am Beispiel der ausgleichenden Geraden | 2008 | 11 0.1 |