
Vermittelnde AusgleichungGenauigkeit ausgeglichener, nicht gemessener Höhendifferenzen
Für ein angeschlossenes Höhennetz geben Sie die Liste der Punkte mit bekannten Höhen an. Die Eingabe der zwei bis vier Spalten folgt den allgemeinen Regeln für tabellarische Eingaben. Die Punktnamen dürfen wie in den gewählt werden. Koordinatenlisten können aus anderen Rechenwerkzeugen geladen werden.
Sollen Höhen als veränderlich angenommen und ausgeglichen werden, geben Sie als Genauigkeitsmaß entweder je eine Standardabweichung oder ein Gewicht an. Wurde ein Ausfallwert für das Genauigkeitsmaß angegeben, füllt er alle fehlenden Werte in der Spalte auf. Andernfalls gelten Höhen ohne Genauigkeitsmaß in der Ausgleichung als fehlerfrei. Das ist gleichbedeutend mit der Standardabweichung Null. Veränderliche Punkte und Festpunkte können gleichzeitig in der Liste vorkommen.
Punkte, die im Netz nicht vorkommen, werden ignoriert. Punkte ohne Höhe oder in der Liste fehlende Netzpunkte werden als Neupunkte betrachtet. Ein freies Höhennetz besteht ausschließlich aus Neupunkten, z.B. wenn die Liste der bekannten Punkte leer ist.
Wenn Sie Koordinaten X und Y angeben, wird das Höhennetz auf der Leinwand dargestellt. Punkte ohne X und Y werden nicht dargestellt. Diese Koordinaten werden nicht in der Netzausgleichung verwendet. Sollen Neupunkte auf der Leinwand erscheinen, müssen Sie auch für diese Punkte Koordinaten X und Y angeben.
Messwerte werden in Form von eingegeben. Beachten Sie auch die Regeln für tabellarische Eingaben. Jeder Messwertsatz beginnt mit zwei Punktnamen, das sind Anfangs- und Endpunktnamen einer Netzlinie. Danach kommen bis zu fünf Messwerte bzw. Genauigkeitsmaße in benutzerdefinierter Reihenfolge.
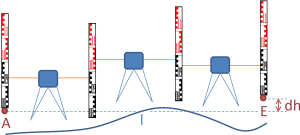
Alle Werte sind immer erforderlich. Fehlende Werte ih, th werden ggf. durch den Ausfallwert aufgefüllt.
Einige oder alle Netzlinien können zweimal gemessen worden sein, nämlich
In diesem Fall sehen Sie auf einer Messwertzeile einfach zwei Spalten für die Höhendifferenz dh oder den Zenitwinkel v vor. Die anderen Größen der Messwertzeile dürfen aber nicht doppelt vorkommen und gelten für beiden Messungen gleichzeitig. Für den dritten Fall gilt: Die Werte von Instrumentenhöhe ih und Zielhöhe th werden nur für AE angegeben und müssen in der Gegensicht EA genau vertauscht sein. Falls das nicht zutrifft, bilden Sie Mittelwerte oder verwenden Sie die nachfolgend beschriebene Methode.
Es ist möglich, aber nicht nötig, beim Rückweg EA das Vorzeichen der Höhendifferenz umzukehren. Für die Höhendifferenz im Hinweg AE wird das Vorzeichen des ersten Wertes angenommen. Also können auch zwei Hinwege gemessen worden sein. Welcher Fall vorliegt, wird an den Vorzeichen des ersten Wertepaares erkannt. Entsprechend wird bei doppelten Zenitwinkeln verfahren. (Theoretisch könnte es passieren, dass die Höhendifferenzen beim ersten Paar so klein sind, dass die Erkennung fehlschlägt. Im Extremfall könnten diese Null sein. Dann sollte eine andere Zeile der Messwertliste an den Anfang verschoben werden.)
Die doppelt gemessenen Netzlinien können in der Messwertliste aber auch zweimal aufgeführt werden. Dieses Vorgehen gestattet höhere Flexibilität. Genauso können mehr als zweimal gemessene Netzlinien eingegeben werden: jede Messung in eine Zeile der Messwertliste.
Beispiele: Die folgenden Eingaben liefern alle dasselbe Ergebnis (rechte Spalte: Winkeleinheit = Gon):
| geometrisches Netz | trigonometrisches Netz |
|---|---|
| // von nach dh1 dh2 l pdh A E 16.10 16.11 2306 1 |
// von nach v1 v2 e ih th pdh A E 92.1402 92.1418 88.2306 1.54 1.66 1 |
| // von nach dh1 dh2 l pdh A E 16.10 -16.11 2306 1 |
// von nach v1 v2 e ih th pdh A E 92.1402 107.8582 88.2306 1.54 1.66 1 |
| // von nach dh l pdh A E 16.10 2306 1 E A -16.11 2306 1 |
// von nach v e ih th pdh A E 92.1402 88.2306 1.54 1.66 1 E A 107.8582 88.2306 1.66 1.54 1 |
Mehrmals gemessene Netzlinien gehen in die Ausgleichung als getrennte Beobachtungen ein, was im Allgemeinen empfohlen wird. Wollen Sie diese als Mittelwerte eingehen lassen, bilden Sie diese Mittelwerte bitte selbst. In den Beispielen oben könnten die Zeilen dann lauten:
| geometrisches Netz | trigonometrisches Netz |
|---|---|
| // von nach dh l pdh A E (16.10+16.11)/2 2306 1 |
// von nach v e ih th pdh A E (92.1402+92.1418)/2 88.2306 1.54 1.66 2 |
Achten Sie darauf, dass mehrmals gemessene Netzlinien nicht als Zwangsbedingung angegeben werden, sonst entsteht ein Widerspruch zwischen den wahrscheinlich ungleichen Werten.
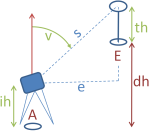
Beobachtungen der Ausgleichung sind hier die gegebenen Höhendifferenzen dh oder die aus Zenitwinkeln v und Distanzen e oder s berechneten Höhendifferenzen sowie die Höhen bekannter, veränderlicher Punkte. Für alle diese benötigt man Genauigkeitsmaße.
Diese Genauigkeitsmaße beziehen sich auch für trigonometrische Höhennetze auf die auszugleichenden Höhendifferenzen dh, schließen also ggf. Messabweichungen in Instrumenten- und Zielhöhen ein.
Korrelierte Beobachtungen werden im Moment noch nicht unterstützt.
Es gibt mehrere Möglichkeiten, wie Sie über die Wahl des Spaltenformats das stochastische Modell festlegen können:
wie oben gegeben oder aus gegebenen Standardabw. oder alle Eins
Zur Festlegung von Gewichten für Höhendifferenzen können indirekt
benutzt werden. Geben Sie dann bitte für jede Netzlinie einen solchen Wert an. Dazu wählen Sie das entsprechende Spaltenformat. Sie können festlegen, wie die Gewichte von den Distanzen oder Linienlängen abgeleitet werden sollen. Jede Höhendifferenz ohne Linienlänge wird als unveränderlich angenommen, so als hätten diese die Standardabweichung Null oder Gewicht ''INF''. Linienlängen müssen nicht in derselben Einheit wie die Höhendifferenzen angegeben sein. Distanzen müssen die Einheit der Höhen und Höhendifferenzen besitzen. Alle Werte müssen positiv sein.
Sollten Sie eine solche Option gewählt haben und zusätzlich noch explizit Standardabweichungen oder Gewichte gegeben haben, erhalten Sie eine Fehlermeldung.
Für Höhen bekannter, veränderlicher Punkte legen Sie ebenfalls eine Standardabweichung in derselben Einheit wie die Höhen oder ein Gewicht wie oben beschrieben fest. Höhen ohne Genauigkeitsmaß oder mit Standardabweichung Null oder Gewicht ''INF'' gelten in der Ausgleichung als fehlerfrei und unveränderlich.
Die Gewichte der Höhen und Höhendifferenzen müssen zueinander passen. Eine Varianzkomponentenschätzung ist im Moment noch nicht implementiert.
Wird den Höhendifferenzen die Standardabweichung Null oder Gewicht ''INF'' zugeordnet, wirken diese als Zwangsbedingungen. Es kann passieren, dass sich solche Zwangsbedingungen widersprechen. Das ist z.B. der Fall, wenn solche Höhendifferenzen
Diese Fälle verursachen einen Fehler. Führen Sie Höhendifferenzen als Zwangsbedingungen mit Bedacht ein.
Die Berechnung erfolgt so, dass entweder der Anfangs- oder der Endpunkt jeder solchen Linie aus der Liste der auszugleichenden Punkte eliminiert und nach der Ausgleichung über die Zwangsbedingung wieder hinzugefügt wird.
Die Ausgleichung erfolgt nach der Methode der kleinsten Quadrate. Freie Höhennetze werden mit der Datumsbedingung ausgeglichen, dass die Summe aller ausgeglichenen Höhen gleich Null ist.
Die dokumentierten Ergebnisse umfassen die Verbesserungen, die ausgeglichenen Werte, deren a posteriori Standardabweichungen und die Redundanzanteile.
Wurden a priori Standardabweichungen für die Höhen und Höhendifferenzen angegeben (z.B. Null), dann errechnet man die a priori Standardabweichungen der ausgeglichenen Größen, indem man die entsprechenden a posteriori Werte durch σo dividiert. Sie finden einen solchen Fall im Beispiel Trigonometrischer Höhenzug.
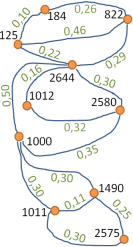
Im dritten Semester werden im Studiengang Geomatik der  Teile des Campus-Höhennetzes durch geometrisches Nivellement gemessen.
Dabei ergaben sich in einem Jahr die unten angegebenen Höhendifferenzen dh
in Meter und Linienlängen l
in Kilometer. Jede Netzlinie wurde mehrfach gemessen, hier zwischen zwei und sechs mal.
Diese Beobachtungen gleichen wir als freies Höhennetz aus.
Teile des Campus-Höhennetzes durch geometrisches Nivellement gemessen.
Dabei ergaben sich in einem Jahr die unten angegebenen Höhendifferenzen dh
in Meter und Linienlängen l
in Kilometer. Jede Netzlinie wurde mehrfach gemessen, hier zwischen zwei und sechs mal.
Diese Beobachtungen gleichen wir als freies Höhennetz aus.
Im Ergebnis erhalten wir für eine einfach gemessene
Linie der Länge 1 km (Gewichtseinheit) eine a posteriori Standardabweichungen von 0.47 mm
. Alle Redundanzanteile liegen über 0.7
, so dass das Netz gut kontrollierbar ist.
Alle Verbesserungen betragen weniger als 0.5 mm
. Für die Punkthöhen ergeben sich a posteriori Standardabweichungen bis maximal 0.15 mm.
| von | nach | Δh [m] | l [km] | von | nach | Δh [m] | l [km] | von | nach | Δh [m] | l [km] |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2580 | 2644 | -0.05638 | 0.37 | 1011 | 2575 | 9.70155 | 0.29 | 822 | 2644 | -2.91135 | 0.28 |
| 2580 | 2644 | -0.05592 | 0.28 | 1000 | 1011 | 8.80803 | 0.29 | 822 | 2644 | -2.91116 | 0.30 |
| 2580 | 2644 | -0.05659 | 0.37 | 1000 | 1011 | 8.80839 | 0.30 | 184 | 822 | 3.11445 | 0.25 |
| 2580 | 2644 | -0.05609 | 0.27 | 1000 | 1011 | 8.80838 | 0.33 | 184 | 822 | 3.11462 | 0.27 |
| 1490 | 2575 | 9.79288 | 0.25 | 1000 | 1011 | 8.80852 | 0.29 | 184 | 822 | 3.11540 | 0.25 |
| 1490 | 2575 | 9.79311 | 0.26 | 1000 | 1490 | 8.71692 | 0.28 | 184 | 822 | 3.11474 | 0.26 |
| 1012 | 2580 | 0.60757 | 0.32 | 1000 | 1490 | 8.71712 | 0.29 | 125 | 184 | 0.61625 | 0.11 |
| 1012 | 2580 | 0.60767 | 0.31 | 1000 | 1490 | 8.71700 | 0.28 | 125 | 184 | 0.61652 | 0.10 |
| 1012 | 2580 | 0.60785 | 0.32 | 1000 | 1490 | 8.71724 | 0.33 | 125 | 184 | 0.61656 | 0.10 |
| 1012 | 2580 | 0.60800 | 0.31 | 1000 | 2580 | -0.60227 | 0.32 | 125 | 184 | 0.61632 | 0.11 |
| 1012 | 2644 | 0.55162 | 0.16 | 1000 | 2580 | -0.60220 | 0.38 | 125 | 184 | 0.61656 | 0.10 |
| 1012 | 2644 | 0.55167 | 0.16 | 1000 | 2580 | -0.60257 | 0.29 | 125 | 184 | 0.61669 | 0.10 |
| 1012 | 2644 | 0.55163 | 0.16 | 1000 | 2580 | -0.60284 | 0.36 | 125 | 822 | 3.73164 | 0.46 |
| 1012 | 2644 | 0.55177 | 0.16 | 1000 | 2644 | -0.65811 | 0.47 | 125 | 822 | 3.73182 | 0.46 |
| 1011 | 1490 | -0.09163 | 0.10 | 1000 | 2644 | -0.65810 | 0.51 | 125 | 2644 | 0.82011 | 0.21 |
| 1011 | 1490 | -0.09118 | 0.12 | 1000 | 2644 | -0.65860 | 0.49 | 125 | 2644 | 0.82042 | 0.22 |
| 1011 | 1490 | -0.09169 | 0.10 | 822 | 2644 | -2.91118 | 0.28 | 125 | 2644 | 0.82039 | 0.28 |
| 1011 | 1490 | -0.09140 | 0.12 | 822 | 2644 | -2.91111 | 0.30 | 125 | 2644 | 0.82062 | 0.22 |
| 1011 | 2575 | 9.70153 | 0.31 |
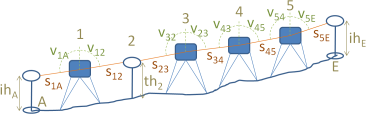
| von | nach | Höhen- differenz |
Schräg- distanz | Ziel- höhe |
|---|---|---|---|---|
| 1 | A | 105.545 | 55.454 | 1.400 |
| 1 | 2 | 95.112 | 71.689 | 1.400 |
| 3 | 2 | 103.230 | 49.528 | 1.400 |
| 3 | 4 | 92.751 | 65.666 | 0.005 |
| 4 | 3 | 107.239 | 65.666 | 0.005 |
| 4 | 5 | 96.345 | 78.300 | 0.005 |
| 5 | 4 | 103.645 | 78.300 | 0.005 |
| 5 | E | 99.300 | 45.650 | 1.400 |
Betrachten wir den abgebildeten Höhenzug mit einem Sprungstand in Punkt 2, d.h. dort befand sich kein Instrumentenstandpunkt und auf Punkt 1 demnach kein Reflektorzielpunkt. Auf den Punkten 3,4,5 befand sich nacheinander der Stand- und der Zielpunkt. Höhen sind für den Anschlusspunkt A mit H=116.10 und für den Abschlusspunkt E mit H=123.06 gegeben. Der Reflektor auf A, 2 und E hat jeweils die Zielhöhe th=1.40 . Die Punkte 1,3,4,5 sind unvermarkt, so dass wir die Höhen jeweils auf die Kippachse des Instruments beziehen: ih=0.00 . Allerdings ist der Reflektorpunkt jeweils 0.005 höher als die Kippachse, so dass auf den Punkten 3,4,5 noch eine Zielhöhe von th=0.005 vorzusehen ist. Die erhaltenen Messwerte finden Sie rechts.
An die Höhendifferenzen werden Verbesserungen mit Beträgen bis maximal 0.0017 angebracht. Die erhaltenen Neupunkthöhen 1,2,3,4,5 erhalten a posteriori Standardabweichungen von höchstens 0.0012.
Dasselbe Beispiel wird auch für den Universalrechner
benutzt und kann damit bearbeitet werden.
Die Ergebnisse sind allerdings nicht völlig identisch, weil
eine robuste Ausgleichung durchführt.
Die Abweichungen in den endgültigen Höhen betragen bis zu 0.0004.
| Punkt- | Höhennetze | Universalrechner | ||
|---|---|---|---|---|
| name | ausgegl. Höhe | Stdabw. | Höhe (Median) | Spannweite |
| 1 | 122.3238 | 9.1e-4 | 122.3238 | 0.0046 |
| 2 | 126.4233 | 0.0012 | 126.4230 | 0.0046 |
| 3 | 130.3350 | 0.0012 | 130.3347 | 0.0046 |
| 4 | 137.7910 | 0.0011 | 137.7906 | 0.0033 |
| 5 | 142.2778 | 7.7e-4 | 142.2779 | 0.0046 |
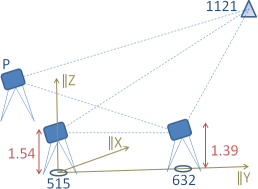
Dieses Beispiel wurde zuvor mit dem Universalrechner bearbeitet. Wir gleichen die Messwerte jetzt als trigonometrisches Höhennetz aus. Dazu benutzen wir die im Universalrechner erhaltenen Schrägdistanzen. Die bekannten Punkthöhen von 515 und 632 werden fest gehalten. Die Lagekoordinaten werden nur für die Darstellung des Netzes auf der Leinwand benutzen.
Bei der Berechnung erhält man die Warnung, dass Beobachtungen zwischen unveränderlichen Festpunkten gefunden und ignoriert wurden. Das sind die beiden Beobachtungen zwischen den Punkten 515 und 632. Alle Beobachtungen sind gut kontrollierbar (Redundanzanteile ≥ 0.45). Die ausgeglichene Höhe des unzugänglichen Punktes 1121 erhalten wir mit 201.1118 und einer Standardabweichung von 0.0014.
Dasselbe Beispiel wird auch für Universalrechner
benutzt und kann damit bearbeitet werden.
Die Ergebnisse sind allerdings nicht völlig identisch, weil
eine robuste Ausgleichung durchführt und alle drei räumlichen Koordinaten bestimmt.
Die Abweichungen in den endgültigen Höhen betragen bis zu 0.07.
Vermittelnde Ausgleichung
und können mit neu ausgeglichen werden. Das bietet folgende Vorteile:
Demnächst werden noch mehr Werkzeuge diese Option bieten.
Die Namen der Beobachtungen sind A°E und die Namen der Parameter sind die Namen der ausgeglichenen Punkte. Wenn Höhendifferenzen als Zwangsbedingungen verwendet wurden, erscheinen diese nicht als Beobachtungen, sondern als Bedingungsgleichungen für Parameter.
Bestimmen Sie die Standardabweichung der ausgeglichenen Höhendifferenz der Punkte 125 und 2575 im Campus-Subnetz der HTW Dresden als freies Nivellementnetz. Lösung: 0.22 mm.
In einem Höhennetz soll die Genauigkeit ausgeglichener, nicht gemessener Höhendifferenzen bestimmt werden. Sie könnten das Höhennetz in laden wie im vorigen Trick und dort die Höhendifferenzen als Funktionen ausgeglichener Parameter (Höhen) angeben. Einfacher ist es, wenn Sie die Höhendifferenzen direkt im Höhennetz als Messwerte mit Gewicht Null oder Standardabweichung ''INF'' angeben. Dann nehmen diese Werte an der Ausgleichung nicht teil, aber Sie erhalten die ausgeglichenen Werte und auch deren Genauigkeiten.
|
|
|
|