
IN DUBIO PRO GEO berechnet ebene und räumliche Koordinatentransformationen, das sind Umrechnungen von Punktkoordinaten eines Quellsystems in Koordinaten eines Zielsystems. Es wird nicht vorausgesetzt, dass die Achsen der Systeme irgendwie näherungsweise ausgerichtet sind. Koordinaten werden über eingegeben.
Kartesische Linkssysteme, kartesische Rechtssysteme (XYZ) und Gittersysteme (Nordwert,Ostwert,Höhe) (oder andere Koordinatenreihenfolge) können unmittelbar transformiert werden. Ellipsoidische Systeme (Länge,Breite,Höhe) müssen erst mit umgerechnet werden. Siehe Koordinatensystemtyp.
Die Koordinaten im Quellsystem werden immer mit x,y,z und die im Zielsystem mit X,Y,Z bezeichnet. Bei Gitterkoordinaten entspricht Nord = x und/oder X, Ost = y und/oder Y und Höhe = z und/oder Z.
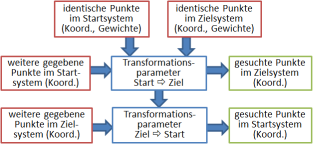
Identische Punkte werden automatisch an identischen Punktnamen erkannt. Wann immer möglich, werden zunächst Transformationsparameter aus diesen Koordinaten berechnet.
Zusätzlich können Punkte vorliegen, die nur in einem der beiden Systeme gegebene Koordinaten haben (Neupunkte). Auf diese Punkte wird die berechnete Transformation angewendet. Neupunkte können zugleich in beiden Systemen vorliegen.
Alle Punkte können in den Koordinatenlisten in beliebiger Reihenfolge angegeben werden.
Alle implementierten geodätischen Koordinatentransformationen werden berechnet, die die folgenden drei Bedingungen erfüllen:
Alle Transformationen gehen von folgendem Grundmuster der Transformationsgleichungen aus:
| V = t + T · v | v , V sind die Ortsvektoren der Punkte im Quell- und Zielsystem. t ist der Translationsvektor (= Verschiebungsvektor). T ist die Transformationsmatrix. |
Die Reihenfolge der Komponenten von v, V, t, T ist immer XYZ, selbst wenn die Koordinaten in den eine andere Reihenfolge haben. Je nach Transformationstyp erzeugt T
Für jede berechnete Transformation werden die Transformationsgleichungen in dieser Form ausgegeben, so dass mit ihnen alle weiteren gewünschten Berechnungen erfolgen können, z.B. die Transformation weiterer Punkte. Oft ist es aber zweckmäßiger, die Transformation durch Transformationsparameter zu beschreiben. Es gibt dazu eine Vielzahl von Möglichkeiten, die hier nahezu vollständig unterstützt werden:
Am einfachsten stellt man T als Produkt von bis zu 3 Matrizen dar:
Die einzelnen Transformationstypen unterscheiden sich nur danach, welche Faktoren T enthält und in welcher Reihenfolge. Bei der Affintransformation kann T in alle drei Faktoren in beliebiger Reihenfolge zerlegt werden:
T = Q1M1S1 = Q2S2M2 = M3S3Q3 = S4M4Q4
Die Faktoren selbst hängen im Allgemeinen von der Reihenfolge der Zerlegung ab, z.B. hätte man S1 ≠ S2 ≠ S3 ≠ S4. Alle genannten Zerlegungen werden berechnet.
Z-Koordinaten oder Höhen werden durch ebene Transformationen nicht beeinflusst, können also auch fehlen. Wenn einige oder alle Punkte in Gittersystemen Höhen besitzen, werden diese nur benutzt, um den Gittermaßstabsfaktor zu bestimmen.
Wann immer möglich, wird im 2D-Fall Folgendes der Reihe nach berechnet:
| Transformation | Parameter | Anzahl | ident.P. | Transformationsmatrix T | |
|---|---|---|---|---|---|
| Affin | tx , ty , mx , my , ε , τ | 6 | ≥ 3 | ist eine allgemeine 2×2 Matrix | |
| 5-Param. Typ 1 | tx , ty , mx , my , ε | 5 | ≥ 3 | hat orthogonale Zeilenvektoren | T=MQ |
| 5-Param. Typ 2 | tx , ty , m , τ , ε | 5 | ≥ 3 | T=mSQ | |
| 5-Param. Typ 3 | tx , ty , ε , mx , my | 5 | ≥ 3 | hat orthogonale Spaltenvektoren | T=QM |
| 5-Param. Typ 4 | tx , ty , m , ε , τ | 5 | ≥ 3 | T=mQS | |
| Helmert | tx , ty , m , ε | 4 | ≥ 2 | ist das skalare Vielfache einer Orthogonalmatrix | T=mQ |
| mit festem Maßstab | tx , ty , ε | 3 | ≥ 2 | ist eine Orthogonalmatrix | T=Q |
Der Translationsvektor t und die Matrizen Q, S, M haben folgende Darstellung:
| t= |
|
ohne Reflexion: |
Q = |
|
mit Reflexion: |
Q = |
|
| S = |
|
= |
|
M = |
|
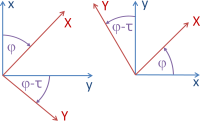
Der Rotationswinkel ε ist der Drehwinkel des Quellsystems ins Zielsystem um den Koordinatenursprung. Im Linkssystem bedeutet ε>0 eine Drehung im Uhrzeigersinn, im Rechtssystem umgekehrt.
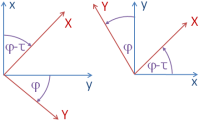
Nach einer Scherung schließen die Achsen des Quellsystems im Zielsystem keinen rechten Winkel mehr ein, sondern einen um den Scherwinkel τ kleineren Winkel oder um -τ größeren Winkel. Im Berechungsprotokoll wird auch der Scherfaktor f = tan(τ) ausgewiesen.
Die Maßstabsfaktoren mx , my sind stets positiv und bei einigen Transformationstypen gleich groß. mx = my = m > 1 bedeutet, dass die Punkte durch die Transformation auseinandergezogen werden. Der oder die Gittermaßstabsfaktoren sind hierin noch nicht enthalten. Ändert man z.B. den Systemtyp von Gitter in kartesisch, ändern sich möglicherweise die berechneten Maßstabsfaktoren.
Alle Punkte müssen hierfür drei Koordinaten besitzen. Wird der Transformationstyp automatisch erkennen gewählt, werden räumliche Transformationen immer dann berechnet, wenn diese Bedingung erfüllt ist und die dritten Koordinaten der gegebenen Punkte nicht alle identisch sind. Andernfalls wird versucht, ebene Transformationen zu berechnen.
Wann immer möglich, wird im 3D-Fall Folgendes der Reihe nach berechnet:
| Transformation | Parameter | Anzahl | ident.P. | Transformationsmatrix T | |
|---|---|---|---|---|---|
| Affin | tx , ty , tz , mx , my , mz , εx , εy , εz , τxy , τxz , τyz | 12 | ≥ 4 | ist eine allgemeine 3×3 Matrix | |
| 9-Param. Typ 1 | tx , ty , tz , mx , my , mz , εx , εy , εz |
9 | ≥ 3 | hat orthogonale Zeilenvektoren | T=MQ |
| 9-Param. Typ 2 | tx , ty , tz , εx , εy , εz , mx , my , mz |
9 | ≥ 3 | hat orthogonale Spaltenvektoren | T=QM |
| Helmert | tx , ty , tz , m , εx , εy , εz | 7 | ≥ 3 | ist das skalare Vielfache einer Orthogonalmatrix | T=mQ |
| mit festem Maßstab | tx , ty , tz , εx , εy , εz | 6 | ≥ 3 | ist eine Orthogonalmatrix | T=Q |
Der Translationsvektor t und die Matrizen S, M haben folgende Darstellungen:
| t= |
|
S = |
|
= |
|
M = |
|
Die 3D-Scherung beschrieben durch S kann man sich als eine Folge von drei ebenen Scherungen vorstellen, und zwar
Wenn man die erste und zweite oder die zweite und dritte ebene Scherung vertauscht, erhält man näherungsweise dieselben Schwerwinkel τij, wenn diese klein sind. Im Berechungsprotokoll werden auch die Scherfaktoren fij = tan(τij) ausgewiesen.
Die 3D-Skalierung hat bis zu drei Maßstabsfaktoren. Die beiden Maßstabsfaktoren bei ebenen Transformationen werden noch um einen dritten Maßstabsfaktor mz ergänzt.
Die Matrix Q ist im Fall ohne Reflexion eine Rotationsmatrix und kann auf folgende drei verschiedenen Arten durch Parameter dargestellt werden:
(a) mit drei Euler-Winkeln εx , εy , εz:
| Q= |
|
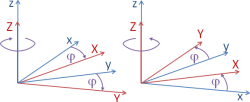
Die gesamte Rotation kann man in eine Folge von drei Rotationen um Koordinatenachsen zerlegen. Wir nutzen hier die geodätische Konvention:
Es sind auch andere Festlegungen gebräuchlich, vor allem in nicht-geodätischen Bereichen.
(b) mit dem Quadrupel der Einheitsquaternion (q0 , q1 , q2 , q3):
| Q= |
|
Eine Quaternion erlaubt in vielen Fällen eine rechnerisch elegantere Beschreibung von Rotationen in drei Dimensionen, als Euler-Winkel. Die vier Parameter genügen der Bedingung q0²+q1²+q2²+q3²=1 (Einheitsquaternion).
(c) mit Euler-Achse (ex , ey , ez) als Einheitsvektor und Rotationswinkel ε um diese Achse:
| Q= |
|
Die Rotation wird hier um eine schräg im Raum liegende Achse durch den Koordinatenursprung beschrieben, die sogenannte Euler-Achse. Die Parameter genügen der Bedingung ex²+ey²+ez²=1 (Einheitsvektor).
Alle Winkel εx, εy, εz, ε werden zwischen -π = -180° = -200 gon und π = 180° = 200 gon in der gewählten Winkeleinheit berechnet. Sie sind
definiert. Der Blick ist hierfür entgegen der Rotationsachse gerichtet. Negative Rotationswinkel ε werden durch Umkehrung der Orientierung der Euler-Achse vermieden.
Es sind auch andere Festlegungen gebräuchlich, vor allem in nicht-geodätischen Bereichen.
Ist schließlich das Quellsystem ein Linkssystem und das Zielsystem ein Rechtssystem oder umgekehrt, muss T zusätzlich noch eine Reflexion erzeugen. Das Anzeichen dafür ist det(T)<0. Wir erreichen dies durch Spiegelung an der yz-Ebene.
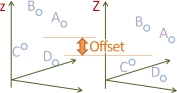
Es wird in diesem Fall vorausgesetzt, dass die vertikalen Achsen (Z oder Höhe) beider Systeme parallel sind und denselben Maßstab haben. Aus allen identischen Punkten, die in beiden Systemen drei Koordinaten besitzen, wird der vertikale Offset berechnet. Mindestens einen solchen Punkt muss es geben. Mit diesem Offset werden nicht-identische Punkte ins jeweils andere System transformiert. Auf die anderen beiden Koordinaten werden möglichst alle oben genannten ebenen Transformationen angewendet.
Sind mehr Koordinaten identischer Punkte vorhanden, als die Transformation Parameter besitzt (Redundanz), erfolgt die Ausgleichung durch die Methode der gewichteten kleinsten Quadrate. In diesem Fall werden Genauigkeitsmaße für die Koordinaten identischer Punkte benötigt, entweder als Standardabweichung σ oder als Gewicht p . Im ersten Fall wird ein Gewicht berechnet entsprechend p=1/σ². Es gibt hierzu zwei verschiedene Modi:
| Gewicht | Std | Die zugehörige Koordinate wird zur Berechnung der Transformationsparameter |
|---|---|---|
| 0 | INF | nicht verwendet. |
| INF oder leeres Feld | 0 oder leeres Feld | als Zwangsbedingung eingeführt. |
Nach der Ausgleichung verbleiben häufig sogenannte Restklaffungen. Diese entsprechen betragsmäßig den Verbesserungen der Ausgleichung, allerdings mit umgekehrtem Vorzeichen:
Restklaffung = gegebene Koordinate − aus Transformationsparametern berechnete Koordinate
Unter der Motorhaube: Intern arbeitet IN DUBIO PRO GEO immer mit den Elementen von t und T als Ausgleichungsparameter. Das sind bei ebenen Transformationen immer 6 und bei räumlichen Transformationen immer 12 Parameter. Bei allen Nicht-Affintransformationen wird die Einschränkung auf spezielle Transformationsmatrizen T durch Bedingungsgleichungen für die Elemente von T vorgenommen. Erst nach der Ausgleichung werden daraus durch QR oder RQ-Faktorisierung von T die Maßstabs-, Scher- und Rotationsparameter berechnet. Insofern sind die Ausgleichungsparameter von den Transformationsparametern zu unterscheiden, außer bei der Affintransformation.
Falls auch die Transformationsparameter der Rücktransformation vom Ziel- ins Quellsystem gebraucht werden, kann die Transformationsrichtung durch Tauschen der Systeme geändert werden. Beachten Sie, dass die Parameter der umgekehrten Transformationen nicht immer durch Ändern der Vorzeichen der Winkel und durch Invertierung der Maßstabsfaktoren erhalten werden.
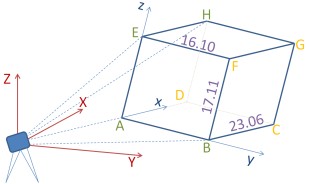
Vier Eckpunkte A,B,E,H eines schräg im Raum liegenden Quaders ABCDEFGH wurden mit Tachymeter gemessen (⇒ Abbildung). Mit einer Standardabweichung von 0.02 wurden die folgenden Koordinaten im Standpunktsystem (kartesisches Linkssystem) X,Y,Z erhalten:
X Y Z A 14.029 17.058 8.073 B 23.616 29.751 5.516 E 14.272 20.210 24.880 H 32.863 6.737 27.163
Für die nicht anzielbaren Punkte C,D,F,G des Quaders sollen die Koordinaten im selben System bestimmt werden.
x y z A 0 0 0 B 0 1 0 C 1 1 0 D 1 0 0 E 0 0 1 F 0 1 1 G 1 1 1 H 1 0 1
Wir führen zusätzlich zum Standpunktsystem xyz ein Objektkoordinatensystem xyz wie oben abgebildet als kartesisches Linkssystem mit Achsen entlang der Kanten des Quaders ein. Allerdings sind die Kantenlängen nicht bekannt. (Die Werte in der Abbildung oben stellen die richtige Lösung dar.) So nehmen wir diese Längen als unbekannte Einheiten der Koordinatenachsen. Damit wird für jede Koordinatenachse eine andere Längeneinheit festgelegt. Nun weisen wir den Punkten A…H die rechts gegebenen Objektkoordinaten zu. Diese nehmen wir als fehlerfrei an.
Die räumliche Transformation vom Objektsystem ins Standpunktsystem muss
bewirken. Die passende Transformation ist also eine 9-Parameter-Transformation Typ 2.
Aus diesen Koordinaten kann nur die Affintransformation und die 9 Parameter Transformation Typ 2 sinnvoll berechnet werden. Für die anderen Transformationen passen die identischen Punkte nicht näherungsweise zusammen (große Restklaffungen).
Die Methode der Kleinsten Quadrate konvergierte nach 3 Iterationen.
| = |
|
+ |
| . |
|
| berechn. | Objektsystem | Standpunktsystem | ||||
|---|---|---|---|---|---|---|
| Punkte | x | y | z | X | Y | Z |
| A | 0 | 0 | 0 | 14.0401824 | 17.0409621 | 8.0693290 |
| B | 0 | 1 | 0 | 23.6010075 | 29.7631971 | 5.5206432 |
| C | 1 | 1 | 0 | 42.1726669 | 16.2649248 | 7.8089579 |
| D | 1 | 0 | 0 | 32.6118418 | 3.5426898 | 10.3576437 |
| E | 0 | 0 | 1 | 14.2835753 | 20.2251565 | 24.8768565 |
| F | 0 | 1 | 1 | 23.8444004 | 32.9473915 | 22.3281707 |
| G | 1 | 1 | 1 | 42.4160598 | 19.4491192 | 24.6164854 |
| H | 1 | 0 | 1 | 32.8552347 | 6.7268842 | 27.1651712 |
| Restkl. | x | y | z | X | Y | Z |
| A | 0 | 0 | 0 | -0.0111824 | 0.0170379 | 0.0036710 |
| B | 0 | 0 | 0 | 0.0149925 | -0.0121971 | -0.0046432 |
| E | 0 | 0 | 0 | -0.0115753 | -0.0151565 | 0.0031435 |
| H | 0 | 0 | 0 | 0.0077653 | 0.0103158 | -0.0021712 |
Die Restklaffungen der Objektsystemkoordinaten x,y,z sind Null, weil diese als fehlerfrei gelten. Die Restklaffungen der Standpunktsystemkoordinaten X,Y,Z betragen maximal 0.017 und sind somit plausibel.
Weisen Sie nach, dass die neuen Standpunktsystemkoordinaten X,Y,Z der 9-Parameter-Transformation Typ 2 genau einen Quader bilden. Hinweis: Koordinaten speichern und in berechnen. Überzeugen Sie sich, dass das mit der Affintransformation nur näherungsweise der Fall wäre.
Nutzen Sie die Schaltfläche , um die entgegengesetzte Transformation zu berechnen. (Javascript darf nicht deaktiviert sein.) Beachten Sie, dass die 9-Parameter-Transformation Typ 1 nun die gesuchte Transformation ist. Die Neupunktkoordinaten sind identisch.
|
|
|
|