
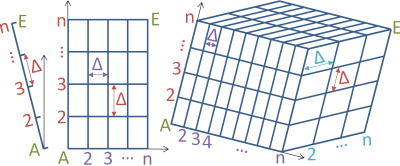
Mit ''Raster'' bezeichnen wir eine Menge regelmäßig angeordneter Punkte. Wir vermeiden hier den Begriff ''Gitter'', weil dieser in der Geodäsie für ein Gittersystem verwendet wird.
Das Raster wird durch einen Anfangspunkt A und einen Endpunkt E definiert. Der erste erzeugte Rasterpunkt ist der Punkt A und der letzte ist der Punkt E. Wenn Sie A und E vertauschen, erhalten Sie dieselben Rasterpunkte in umgekehrter Reihenfolge.
| Raster | Eigenschaft | eben oder räumlich |
|---|---|---|
| Linie (1D) Mehr erfahren |
Auf der Verbindungslinie AE werden gleichabständige Zwischenpunkte erzeugt. Die Linie kann beliebig schräg im Raum verlaufen. | A und E müssen beide 2D- oder beide 3D-Punkte sein, und so werden auch die Zwischenpunkte erzeugt. |
| Rechteck (2D) Mehr erfahren |
Im von A und E aufgespannten achsparallelen horizontalen Rechteck werden in beiden Achsrichtungen gleichabständige Zwischenpunkte erzeugt. | Sind A und E beide 2D-Punkte, so werden auch 2D-Zwischenpunkte erzeugt. Hat A oder E drei Koordinaten, so wird die dritte Koordinate auf alle Zwischenpunkte übertragen. Sind A und E beide 3D-Punkte, so müssen die dritten Koordinaten überein stimmen. |
| Quader (3D) Mehr erfahren |
Im von A und E aufgespannten achsparallelen Quader werden in allen drei Achsrichtungen gleichabständige Zwischenpunkte erzeugt. | A und E müssen beide 3D-Punkte sein, und so werden auch die Zwischenpunkte erzeugt. |
Nur bei kartesischen Koordinaten (XYZ) liegen die Rasterpunkte räumlich gesehen immer auf Geraden und sind im euklidischen Sinne gleichabständig. Sonst ist diese Eigenschaft nur nach Abbildung in die Koordinatenebene gegeben. Z.B. bei ellipsoidischen Koordinaten (Breite, Länge) liegen diese auf Meridianen oder Parallelkreisen oder auf der Loxodrome. Exakte Gleichabständigkeit wird hier nur in der Rektangularprojektion erreicht. Siehe hierzu Koordinatensystemtyp und Loxodrome von Dresden (Sachsen) nach Dresden(Ontario).
Für die Linienrichtung (1D-Raster) oder jede Achsrichtung (2D- oder 3D-Raster) werden in beliebiger Reihenfolge drei Eingabegrößen verlangt. Folgende fünf Größen stehen zur Wahl:
Eine gegebene Kantenlänge muss immer mit genau einer Koordinate von A oder E kombiniert werden. Bei negativer Kantenlänge durchlaufen die Rasterpunkte die zugehörige Achse in entgegengesetzter Richtung, beginnen also mit der größten Koordinate.
Punktanzahlen und Rasterweiten sollten nicht Null sein, sonst wirken sie wie eine fehlende Eingabe.
Beispiel: Das Raster mit den Koordinaten X=11;21;31;41 kann auf folgende Weisen definiert werden:
| XA=11; XE=41; n=4 | XA=11; n=4; l=30 | XA=41; XE=11; n=4 | XA=41; n=4; l=-30 |
| XA=11; XE=41; Δ=10 | XE=41; n=4; l=30 | XA=41; XE=11; Δ=-10 | XE=11; n=4; l=-30 |
| XA=11; n=4; Δ=10 | XA=11; Δ=10; l=30 | XA=41; n=4; Δ=-10 | XA=41; Δ=-10; l=-30 |
| XE=41; n=4; Δ=10 | XE=41; Δ=10; l=30 | XE=11; n=4; Δ=-10 | XE=11; Δ=-10; l=-30 |
| Ergebnis: X=11;21;31;41 | Ergebnis: X=41;31;21;11 | ||
Wenn die Kantenlänge kein ganzzahliges Vielfaches der Rasterweite ist, wird die Rasterweite angepasst. So erhält man das Beispiel-Raster auch mit XA=11; XE=41; Δ=9 oder XE=41; Δ=11; l=30.
Auch beim Gittersystem haben Rasterweite und Kantenlänge den metrischen Maßstab, sind also nicht mit dem Gittermaßstabsfaktor behaftet. Wenn das unerwünscht ist, deklarieren Sie bitte das System vorübergehend als kartesisches System XYZ oder YXZ. Siehe auch Messwertlisten mit Distanzen etc. im Gittermaßstab .
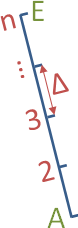
Die Rasterpunkte sind gleichabständige Punkte auf dem Geradenstück AE, die schräg im Raum verlaufen kann. Hier müssen die Eingabegrößen immer A- und E-Koordinaten sowie entweder die Punktanzahl n oder die Rasterweite Δ sein. Die ersten beiden Spalten der Eingabewerte müssen vollständig ausgefüllt sein, wobei die zweite Punktanzahl n=1 oder die Rasterweite Δ=0 gesetzt wird.
Die Rasterweite ist der Abstand benachbarter Punkte. Bei ellipsoidischen Systemen wird die Höhe, soweit vorhanden, nicht in die Abstandsberechnung einbezogen. Siehe Loxodrome von Dresden (Sachsen) nach Dresden (Ontario).
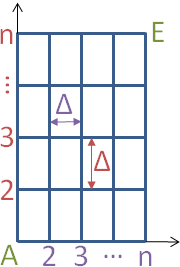
Die Rasterpunkte liegen auf den Schnittpunkten gleichabständiger Koordinatenlinien, bilden also ein achsparalleles Rechteck-Raster. Die ersten beiden Spalten der Eingabewerte müssen vollständig ausgefüllt sein.
Das 2D-Raster kann nach seiner Erzeugung gedreht werden. Für andere Transformationen können Sie die Rasterpunkte in laden. Siehe 2D-Raster für den Großen Garten Dresden.
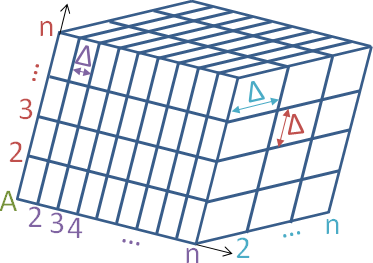
Die Rasterpunkte liegen auf den Schnittpunkten gleichabständiger Koordinatenebenen, bilden also ein achsparalleles Quader-Raster. Alle neun Eingabewerte müssen vollständig angegeben werden. Auf der Leinwand wird nur eine Rasterebene dargestellt (dritte Koordinate fest).
Sie können auch ein vertikales 2D-Raster erzeugen, nämlich als 3D-Raster mit der Punktanzahl n=1 für die erste oder zweite Koordinate. Allerdings müssen dann diese Koordinaten von A und E gleich sein. Schließlich können Sie sogar ein vertikales 1D-Raster erzeugen, wenn die erste und zweite Punktanzahl gleich 1 ist und sich A und E nur in der dritten Koordinate unterscheiden. Dasselbe Raster erhält man als echtes 1D-Raster mit nur einer Punktanzahl oder Rasterweite aber einfacher.
Das 3D-Raster kann nach seiner Erzeugung um eine vertikale Achse gedreht werden. Für andere Transformationen können Sie die Rasterpunkte in laden.
Der erste erzeugte Rasterpunkt ist der Punkt A und der letzte ist der Punkt E. Wenn Sie A und E vertauschen, erhalten Sie dieselben Rasterpunkte in umgekehrter Reihenfolge.
Die erzeugten Rasterpunkte werden zu einer Koordinatenliste zusammengestellt. Sie vergeben einen Systemnamen und legen einen Systemtyp fest. Das Spaltenformat ist immer ''Koordinaten'', so dass die erzeugten Rasterpunkte automatisch benannt werden. Rasterpunktlisten können gespeichert und mit anderen Rechenwerkzeugen weiter verarbeitet (z.B. gedreht) werden.
Dieses Drehen ist für ellipsoidische Koordinaten (Breite, Länge) nicht möglich. Andernfalls können Sie wählen, ob Rasterpunkte um eine vertikale Achse (parallel zur z-Achse) gedreht werden sollen, und um welchen Punkt. Folgende stehen zur Auswahl:
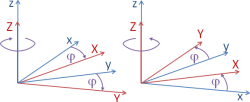
Nach Erzeugen des achsparallelen Rasters oder 1D-Rasters geben Sie den Rotationswinkel zwischen -π = -180° = -200 gon und π = 180° = 200 gon. Die Winkeleinheit sollten Sie zuvor in den spezifiziert haben. Rotationen sind
definiert. Der Blick ist hierfür entgegen der Rotationsachse gerichtet, also von oben.
Für andere Transformationen, z.B. Rotationen um andere Achsen oder Scherungen, können Sie die Rasterpunkte in laden und dort beliebige Transformationsschritte und Parameter konfigurieren.
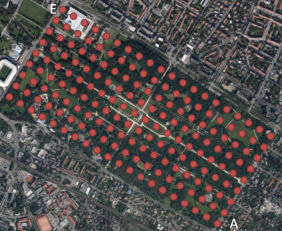
Der Große Garten Dresden hat einen etwa rechteckigen Grundriss mit den Seitenlängen 1900 m und 950 m. Der nördliche Eckpunkt hat die UTM-Koordinaten (Zone 33U) Ostwert = 412734 m und Nordwert = 5655664 m. Der Richtungswinkel der kurzen Seite beträgt 35 gon ≈ 31°. Ein Raster mit der Rasterweite 190 m soll berechnet werden.
Zunächst erzeugt man für den Gittersystemtyp Ostwert Nordwert Höhe ein achsparalleles 2D-Raster über einem Rechteck mit den Kantenlängen 1900 m; 950 m und den Rasterweiten 190 m in beiden Achsrichtungen. Damit das Raster im nördlichen Eckpunkt E endet, kann man die erste Kantenlänge und die erste Rasterweiten negativ angeben, so dass die erste Koordinate (Ost) entgegen der Achsrichtung durchlaufen wird. Nach dem Erzeugen entstehen 11×6=66 Rasterpunkte. Schließlich muss das Raster noch um 31° um Punkt E gedreht werden.
Wir betrachten folgende Punkte in ellipsoidischen Koordinaten bezogen auf :
| ellipsoidische | |||
|---|---|---|---|
| Punkt | Breite | Länge | Höhe |
Dresden (Sachsen), Mittelpunkt des Zentralgebäudes der 
| 51.037512° | 13.735186° | 120 m |
| Dresden (Ontario), St. Andrews Presbyterian Church | 42.590278° | -82.181667° | 183 m |
Zwischen diesen Punkten soll die Loxodrome über Zwischenpunkte realisiert werden. Als Abstand der Zwischenpunkte wählen wir 1°.
Überzeugen Sie sich davon, dass die Punkte auf dem Ellipsoid keineswegs genau gleichabständig sind, indem Sie die erzeugten 97 Punkte in laden und als Polylinie auf dem Ellipsoid berechnen. Die Seitenlängen variieren zwischen 70826 m und 82532 m. Außerdem erkennen Sie, dass die Loxodrome nicht die kürzeste Verbindung zwischen den Punkten auf dem Ellipsoid ist, denn alle Polygonwinkel sind kleiner als π = 180° = 200 gon. Der kleinste Polygonwinkel ist der erste mit 199.12 gon = 179.21°.
Statt dessen haben wir gleichabständige Zwischenpunkte auf einer Geraden in Rektangularprojektion erzeugt. Um das zu beweisen, laden Sie die erzeugten Punkte in eine Koordinatenliste und ändern den Systemtyp in XYZ oder YXZ vor dem Speichern. Nun laden Sie die gespeicherte Liste in und berechnen diese als Polylinie. Die Höhen werden jetzt ignoriert. Die Seitenlängen sind nun alle gleich 1.0030010552°. Die Differenz zum gewünschten Wert Δ=1° kommt dadurch zustande, dass die eingestellte Rasterweite kein ganzzahliges Vielfaches des Punktabstandes ist, so dass die Rasterweite geringfügig angepasst werden musste. Alle ebenen Polygonwinkel sind nun exakt gleich π = 180° = 200 gon.
Nun laden Sie diese Liste auch in , um zu sehen, dass die Punkte auch im 3D-Raum gleichabständig sind. Der Abstand von 1.1986138574 ist nun jedoch eine merkwürdige Mischung aus Grad und Meter. Alle räumlichen Polygonwinkel sind erneut exakt gleich π = 180° = 200 gon.
Vergleichen Sie die Lösungen dieser Aufgaben mit Punkte auf der geodätischen Linie von Dresden (Sachsen) nach Dresden (Ontario).
|
|
|
|